Coin MATHÉMATIQUES
+11
Carlobservateur
Bastien
Julien
Paul
Peyo13
Anonyme
bibi6
rhyolite
RiverOfBoyards
garsim
Pix
15 participants
Page 7 sur 8
Page 7 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8 
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
@Carlobservateur : Sans vouloir être méchant, le but de ce sujet n'est pas de faire des maths juste pour dire d'en faire ! C'est nettement plus intéressant lorsque les maths sont un outil pour répondre à un problème naturel (cc @garsim). C'est d'ailleurs ce que j'ai presque toujours fait dans ce sujet et dans le jeu Mathématiques boyardesques (à part les énigmes de mon FBV, qui elles étaient totalement artificielles et n'avaient été créées dans le seul but d'être résolubles rapidement - en théorie ^^).
Dans ce que tu postes, le biathlon n'est qu'un prétexte pour faire faire des maths à des collégiens. Si encore le thème avait été Fort Boyard j'aurais compris, mais là ce sont avant tout de simples exos de maths autour desquels on a un peu brodé pour rendre ça un tout petit peu plus ludique (et encore).
Si vous voulez, je peux vous faire partager le dernier devoir que j'ai fait, mais je doute que les formes symplectiques intéressent grand monde ici !
Voilà un exemple de cadre qui est une vraie mine de problèmes mathématiques concrets (et surtout non triviaux) : The Wall !

Pour une fois je ne vais rien ajouter de plus pour le moment. Je trouve que ça peut être intéressant de vous laisser vous poser des questions sur ce nouveau jeu, puis éventuellement essayer d'y répondre en modélisant la situation.
D'ailleurs, même si vous n'avez absolument aucune idée de comment y répondre - et même si vous n'y connaissez rien en maths ^^, n'hésitez pas à poser vos questions qui vous viennent naturellement en tête ici (en rapport avec les maths bien sûr), on essaiera de trouver la solution.
Dans ce que tu postes, le biathlon n'est qu'un prétexte pour faire faire des maths à des collégiens. Si encore le thème avait été Fort Boyard j'aurais compris, mais là ce sont avant tout de simples exos de maths autour desquels on a un peu brodé pour rendre ça un tout petit peu plus ludique (et encore).
Si vous voulez, je peux vous faire partager le dernier devoir que j'ai fait, mais je doute que les formes symplectiques intéressent grand monde ici !
Voilà un exemple de cadre qui est une vraie mine de problèmes mathématiques concrets (et surtout non triviaux) : The Wall !

Pour une fois je ne vais rien ajouter de plus pour le moment. Je trouve que ça peut être intéressant de vous laisser vous poser des questions sur ce nouveau jeu, puis éventuellement essayer d'y répondre en modélisant la situation.
D'ailleurs, même si vous n'avez absolument aucune idée de comment y répondre - et même si vous n'y connaissez rien en maths ^^, n'hésitez pas à poser vos questions qui vous viennent naturellement en tête ici (en rapport avec les maths bien sûr), on essaiera de trouver la solution.
- Spoiler:
- Désolé, c'est encore des probas

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Un très facile pour débuter !
Je place ma boule en position 4 et je suppose qu'elle a autant de chances d'aller à gauche ou à droite à chaque clou ou rebord en bas de mur atteint.
Ma question est simple : combien ai-je de chances d'atteindre le 1 tout à droite du mur ?
Je place ma boule en position 4 et je suppose qu'elle a autant de chances d'aller à gauche ou à droite à chaque clou ou rebord en bas de mur atteint.
Ma question est simple : combien ai-je de chances d'atteindre le 1 tout à droite du mur ?

Chris K. is watching you, avec modération bien sûr ^^

Julien- Fan-Accro

- Inscription : 03/12/2011
Messages : 2224
Boyards : 3676
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je suppose que c'est pas ça mais (1/2) exposant 14 soit 1/16384?

"Carpe Diem" Dead Poets Society
"Keep your lovin' brother happy" Once Upon A Time In The West
"Name a shrub after me; something prickly and hard to eradicate" Master and Commander: The Far Side of The World
"Shadows and dust" Gladiator
"Faith is a gift that I have yet to receive" Angels and Demons
"There should be no boundaries to human endeavor. We are all different. However bad life may seem, there is always something you can do, and succeed at. While there's life, there is hope. " The Theory of Everything
"Keep your lovin' brother happy" Once Upon A Time In The West
"Name a shrub after me; something prickly and hard to eradicate" Master and Commander: The Far Side of The World
"Shadows and dust" Gladiator
"Faith is a gift that I have yet to receive" Angels and Demons
"There should be no boundaries to human endeavor. We are all different. However bad life may seem, there is always something you can do, and succeed at. While there's life, there is hope. " The Theory of Everything

RiverOfBoyards- Fan-Illuminé(e)

- Inscription : 14/05/2016
Messages : 448
Boyards : 453
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Et pourtant c'est ça, car il y a 2^14 chemins possibles, et pour aller en 1 à droite pas le choix faut toujours aller à droite, donc un seul chemin 

Chris K. is watching you, avec modération bien sûr ^^

Julien- Fan-Accro

- Inscription : 03/12/2011
Messages : 2224
Boyards : 3676
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
C'est en effet le cas le plus simple, ça me paraît une bonne idée de commencer par bien étudier celui-là avant de passer aux autres.Julien a écrit:Je place ma boule en position 4
C'est le modèle mathématique le plus classique pour ce genre de jeu, et c'est celui qu'on utilisera tout du long. Certes il n'est pas forcément parfaitement fidèle à la réalité (on a déjà vu des boules rebondir et se déplacer horizontalement de quelques cases), mais au moins il donne une idée assez précise des probas en jeu ici.Julien a écrit:je suppose qu'elle a autant de chances d'aller à gauche ou à droite à chaque clou ou rebord en bas de mur atteint.
J'ajoute tout de même que l'on supposera systématiquement que chaque direction (gauche ou droite) est tirée au sort indépendamment des précédentes. Je me doute que c'était sous-entendu, mais c'est important de le préciser sinon on ne peut pas faire grand chose ^^
Questions un peu plus difficiles que la première - mais rien de bien méchant non plus, et toujours en supposant que la boule est lâchée en position 4 :
Quelle est la probabilité de tomber dans l'avant-dernière trappe (celle à 150 000 € sur la capture) ?
Plus généralement, si on numérote les trappes de 0 à 14 de gauche à droite, quelle est la probabilité de tomber dans la trappe n° k ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
La logique veut qu'il y ait 14 chances sur 16384 que la boule puisse aller en 1 ou en 13, c'est à dire sur 5 000 ou 150 000 ^^
Le reste, j'en sais rien XD
Le reste, j'en sais rien XD


Quentin- Fan-Imbattable

- Inscription : 06/07/2013
Messages : 4231
Boyards : 6745
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Quentin a écrit:La logique veut qu'il y ait 14 chances sur 16384 que la boule puisse aller en 1 ou en 13, c'est à dire sur 5 000 ou 150 000 ^^
Wow, je ne m'attendais vraiment pas à te voir un jour poster sur ce sujet !

Il y a plusieurs manières de voir les choses. L'une d'elle est de résumer le trajet de la boule en 14 étapes, que l'on peut représenter par 14 cases. Chaque case accueille soit gauche (◄), soit droite (►). Pour arriver dans la case 13, il faut exactement 1 ◄ et le reste en ►, soit exactement 14 possibilités. Le nombre d'issues total est 214, et comme elles sont toutes équiprobables on arrive bien à une proba de 14/214, soit environ 1 chance sur 1170, ou encore 0,09 %. C'est pas beaucoup
Évidemment on a le même résultat pour la case 1.
Pour le cas général c'est exactement le même raisonnement, si ce n'est que le dénombrement du nombre d'issues favorables ne peut plus se faire facilement "à la main" et qu'il vaut mieux utiliser un outil bien pratique dont on a déjà pas mal parlé sur le forum...

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Pixelax a écrit:Julien a écrit:je suppose qu'elle a autant de chances d'aller à gauche ou à droite à chaque clou ou rebord en bas de mur atteint.
[...]
J'ajoute tout de même que l'on supposera systématiquement que chaque direction (gauche ou droite) est tirée au sort indépendamment des précédentes. Je me doute que c'était sous-entendu, mais c'est important de le préciser sinon on ne peut pas faire grand chose ^^
Oui, enfin... si on n'a pas ces hypothèses, on dit adieu aux théories de la loi binomiale
(Certes, l'hypothèse de Julien est un peu forte, mais au moins... il faut, pour pouvoir appliquer la théorie de la loi binomiale, qu'à chaque clou, on ait ume même proba $p$ d'aller à gauche, par exemple - et du coup, $1-p$ de proba d'aller à droite).
Du coup, si j'ai bien lu vos posts précédents... on est sur B(14, 1/2). Et assez naturellement là-dedans, y'a l'outil évoqué par Pixelax

bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
Boyards : 1275
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Ça ne sert à rien de mettre des "$" dans tes formules ici : soit tu utilises du LaTeX et tu insères les résultats compilés - via des images, soit tu fais sans et tu enlèves tout le superflu (à la rigueur tu peux mettre les maths en italique si tu préfères, et/ou utiliser des symboles unicodes quand ils existent) ^^bibi6 a écrit:Oui, enfin... si on n'a pas ces hypothèses, on dit adieu aux théories de la loi binomiale
(Certes, l'hypothèse de Julien est un peu forte, mais au moins... il faut, pour pouvoir appliquer la théorie de la loi binomiale, qu'à chaque clou, on ait ume même proba $p$ d'aller à gauche, par exemple - et du coup, $1-p$ de proba d'aller à droite).
Attention, il ne faut pas partir d'un modèle mathématique et tout faire pour que notre problème réel rentre dans ce cadre ! Je n'aime pas vraiment qu'on dise "il faut supposer ça, on n'a pas le choix", c'est pas comme ça que ça marche ^^
On part de notre problème réel, et on le modélise mathématiquement. À ce moment là on fait nécessairement des choix - plus ou moins fidèles à la réalité - et ensuite on voit ce qu'on peut dire avec les hypothèses que l'on a faites.
Là ce n'est pas un exercice "scolaire" dans le sens où l'on vient de voir un super résultat théorique, et où l'énoncé fait tout pour inciter les élèves à utiliser ce résultat. C'est justement pour éviter ça que j'ai lancé le sujet sans imposer aucune hypothèse, pour voir les initiatives que vous alliez prendre.
Donc ici, rien ni personne n'oblige à utiliser la loi binomiale à la base, on peut tout à fait traiter ce problème sans, notamment si on fait des hypothèses plus faibles. Évidemment, ça peut devenir nettement plus compliqué, donc c'est une bonne idée de se placer dans un cadre adéquat pour en parler ici, et pour donner une idée des probas en jeu. Mais il faut bien être convaincu qu'une fois le modèle fixé, tout en découle. Si des résultats semblent incohérents avec ce que l'on obtient en pratique, c'est lui qu'il faudra remettre en cause, et non la théorie mathématique qu'il y a derrière.
Bref, tout ça pour dire que c'est très important de préciser clairement toutes les hypothèses que l'on fait avant de se lancer dans des calculs ou des démonstrations. L'indépendance est absolument fondamentale dans le modèle choisi, tout est basé là dessus. Mais soyez conscients qu'on peut très bien se débrouiller sans (avec d'autres hypothèses traduisant la dépendance à la place, par exemple une boule a 3 chances sur 4 de continuer dans la même direction), on obtiendrait alors un autre modèle qui donnerait des résultats différents
Ceci étant dit, revenons à nos moutons ! ^^
Effectivement on a bien à faire à une loi binomiale ici, de paramètres 14 et 1/2. Mais bon, vu comment mes questions étaient tournées, j'attendais que l'on retrouve le résultat plutôt qu'on le balance directement et qu'on remonte pour répondre aux questions intermédiaires !
Si je fais ça c'est surtout pour essayer de faire comprendre pourquoi on a une telle expression générale à ceux qui n'ont pas forcément l'habitude des probas. Et comme on a des scenarii équiprobables ici, je pense que c'est bien d'insister sur le raisonnement basé sur le dénombrement des issues. Parce que quand la loi n'est pas usuelle (comme la loi de la cellule qui rétrécit), ben on n'a pas le choix !
Ici, le seul outil dont on a besoin ce sont les coefficients binomiaux (là je ne vois pas comment on peut s'en passer). Je rappelle donc que le coefficient binomial
C'est exactement ce dont on a besoin, puisque si l'on va dans la trappe k, c'est qu'on est allé exactement k fois à droite. Cela revient à choisir sur nos 14 cases traduisant le parcours de la boule k cases qui accueilleront un ►. Dans les autres il ne pourra alors y avoir que des ◄. Soit
Comme on a 214 issues au total, on obtient finalement (en notant X le numéro de la trappe d'arrivée) :
Bon je vous l'accorde, c'est pas très parlant !
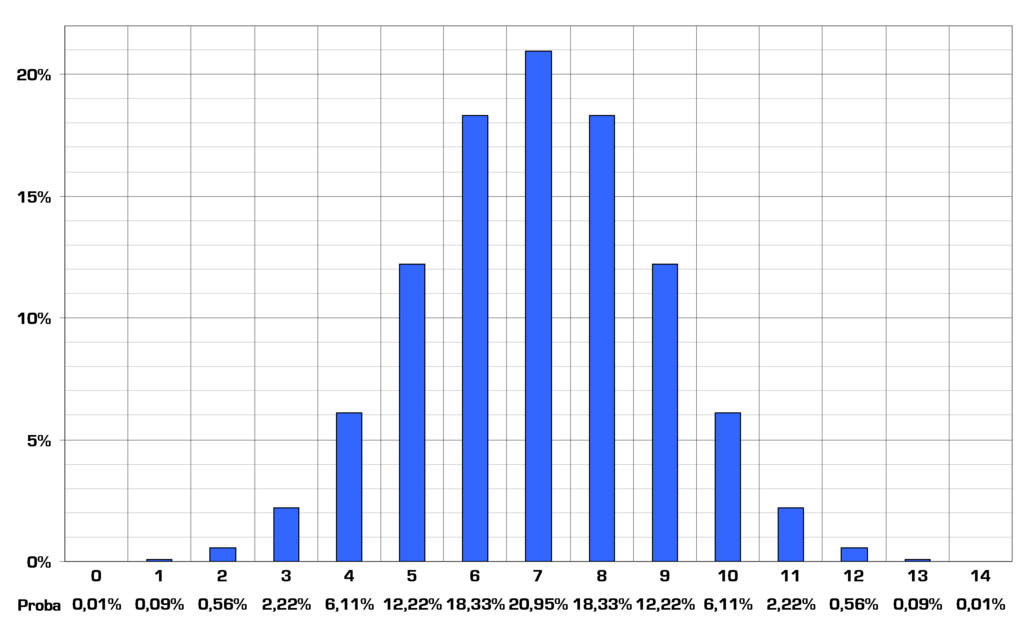
On peut du coup calculer le gain moyen, avec une boule lâchée en 4 :
En manche 1 : 1 584 €
En manche 2 : 5 807 €
En manche 3 : 15 084 €
Je précise que ces valeurs numériques (celles du graphique et les gains moyens) sont bien entendu des valeurs approchées.
Bon on n'a rien inventé, c'est quelque chose d'assez connu en probabilités, sous le nom de planche de Galton (ou Bean machine in english). Si ça vous intéresse il y a pas mal d'animations disponibles en ligne, qui illustrent bien la théorie.
Avant de passer au cas général (où la boule n'est pas forcément lâchée en 4), j'ai une autre petite question pour vous : quelle est la probabilité de tomber dans une trappe impaire (i.e. une grosse somme) ? Comment montrer ce résultat sans utiliser d'application numérique ?
Je rappelle en passant que ça peut être dangereux d'additionner des valeurs approchées car les erreurs peuvent s'accumuler... #JDCJDR

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Pixelax a écrit:Ça ne sert à rien de mettre des "$" dans tes formules ici : soit tu utilises du LaTeX et tu insères les résultats compilés - via des images, soit tu fais sans et tu enlèves tout le superflu (à la rigueur tu peux mettre les maths en italique si tu préfères, et/ou utiliser des symboles unicodes quand ils existent) ^^bibi6 a écrit:Oui, enfin... si on n'a pas ces hypothèses, on dit adieu aux théories de la loi binomiale
(Certes, l'hypothèse de Julien est un peu forte, mais au moins... il faut, pour pouvoir appliquer la théorie de la loi binomiale, qu'à chaque clou, on ait ume même proba $p$ d'aller à gauche, par exemple - et du coup, $1-p$ de proba d'aller à droite).
C'est pas faux... c'est plus par habitude ^^
PixelaxAttention, il ne faut pas partir d'un modèle mathématique et tout faire pour que notre problème réel rentre dans ce cadre ! [...]
On part de notre problème réel, et on le modélise mathématiquement. À ce moment là on fait nécessairement des choix - plus ou moins fidèles à la réalité - et ensuite on voit ce qu'on peut dire avec les hypothèses que l'on a faites.
Tout à fait d'accord avec toi - il est vrai que mon message précédent laisse supposer que je veux absolument la loi binomiale derrière...
Pixelax a écrit:Là ce n'est pas un exercice "scolaire" dans le sens où l'on vient de voir un super résultat théorique, et où l'énoncé fait tout pour inciter les élèves à utiliser ce résultat. C'est justement pour éviter ça que j'ai lancé le sujet sans imposer aucune hypothèse, pour voir les initiatives que vous alliez prendre.
Donc ici, rien ni personne n'oblige à utiliser la loi binomiale à la base, on peut tout à fait traiter ce problème sans, notamment si on fait des hypothèses plus faibles.[...]
... mais, faut avouer, que tu y pensais fortement!
Pixelax a écrit:Bref, tout ça pour dire que c'est très important de préciser clairement toutes les hypothèses que l'on fait avant de se lancer dans des calculs ou des démonstrations. L'indépendance est absolument fondamentale dans le modèle choisi, tout est basé là dessus. Mais soyez conscients qu'on peut très bien se débrouiller sans (avec d'autres hypothèses traduisant la dépendance à la place, par exemple une boule a 3 chances sur 4 de continuer dans la même direction), on obtiendrait alors un autre modèle qui donnerait des résultats différents
Sauf que ce serait plus compliqué à mettre en place ^^ - sinon, je suis encore tout à fait d'accord avec toi: la précision des hypothèses est sans doute le plus important. Et c'était le but de mon message précédent
Pixelax a écrit:Ceci étant dit, revenons à nos moutons ! ^^
Effectivement on a bien à faire à une loi binomiale ici, de paramètres 14 et 1/2. Mais bon, vu comment mes questions étaient tournées, j'attendais que l'on retrouve le résultat plutôt qu'on le balance directement et qu'on remonte pour répondre aux questions intermédiaires !
Désolé...
Pixelax a écrit:[size=10][size=13]Avant de passer au cas général (où la boule n'est pas forcément lâchée en 4), j'ai une autre petite question pour vous : quelle est la probabilité de tomber dans une trappe impaire (i.e. une grosse somme) ? Comment montrer ce résultat sans utiliser d'application numérique ?
Je rappelle en passant que ça peut être dangereux d'additionner des valeurs approchées car les erreurs peuvent s'accumuler... #JDCJDR [/size][/size]
Sur le coup, j'aurais dit 1/2, mais je me rends compte en postant que mon argument est bancal. Je réfléchis et je reviens

bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
Boyards : 1275
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES





Dominique Lebreton en 1990 dans l'épreuve du Sable :
"Alors je vois du sable...je pense que la clé doit être dans le sable...alors j'vais prendre la pelle... -AH BAH IL A TOUT COMPRIS- et je vais le jeter par la fenêtre ! -MAIS NON MAIS NON PAS PAR LA FENÊTRE !!! MAIS QU'EST-CE QU'IL FAIT ?!-"

Lumiere_Du_Fort- Fan-Habitué(e)

- Inscription : 24/02/2017
Messages : 295
Boyards : 412
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
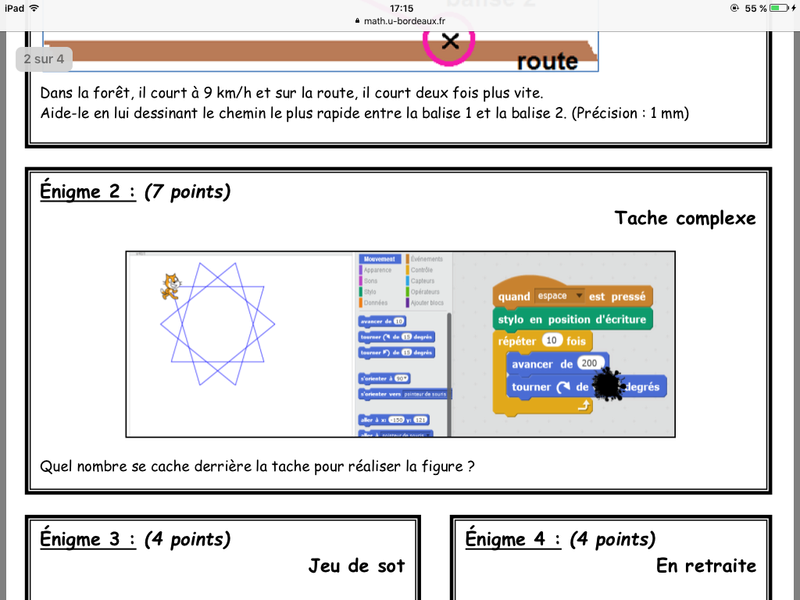
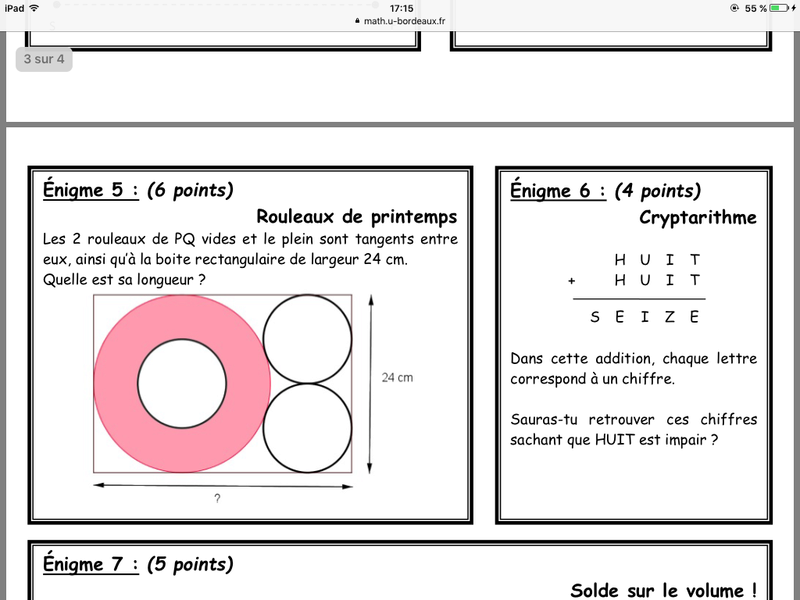
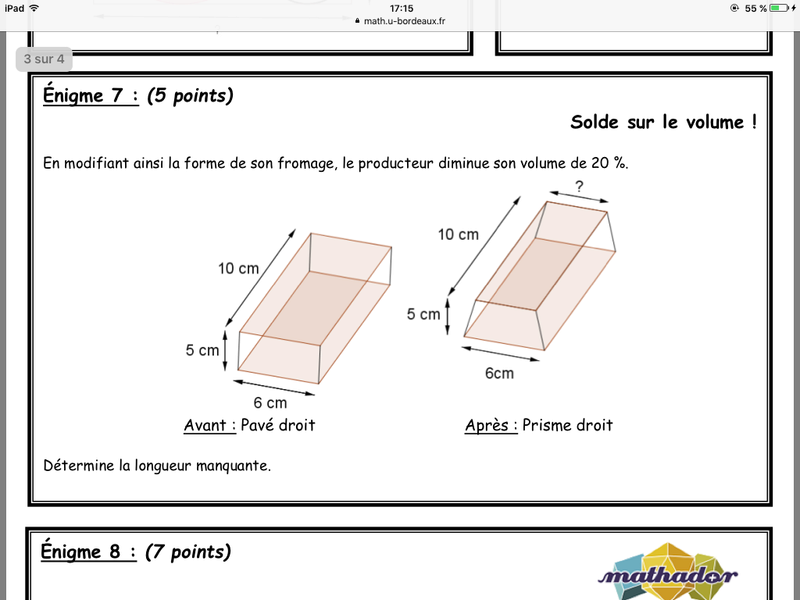
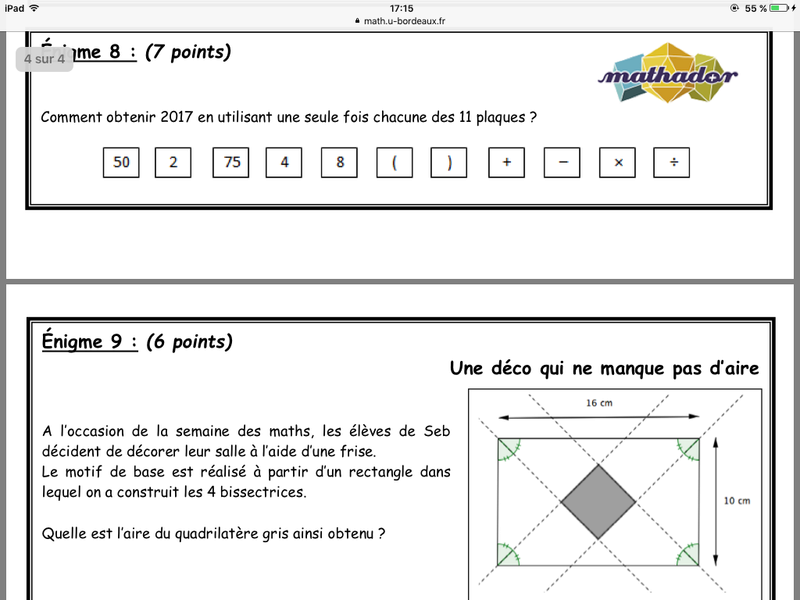
Voila si ca en intéresse ici, je partage avec vous les 12 énigmes qui ont été posées à des classes de secondes durant le concours "Rallye-Math", session mars 2017. 

Dominique Lebreton en 1990 dans l'épreuve du Sable :
"Alors je vois du sable...je pense que la clé doit être dans le sable...alors j'vais prendre la pelle... -AH BAH IL A TOUT COMPRIS- et je vais le jeter par la fenêtre ! -MAIS NON MAIS NON PAS PAR LA FENÊTRE !!! MAIS QU'EST-CE QU'IL FAIT ?!-"

Lumiere_Du_Fort- Fan-Habitué(e)

- Inscription : 24/02/2017
Messages : 295
Boyards : 412
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Et sinon, si ça intéresse quelqu'un, j'ai passé l'écrit de l'agrégation externe spécial hier. Neuf exercices variés, et deux problèmes dont un seul était à choisir et à traiter. Celui que j'ai choisi concernait les principes d'incertitude sur un groupe abélien fini (et le lien est la mécanique quantique); l'autre était sur les mesures cristallines (voir "Espace de Schwartz").
Bon, et avec tout ça, j'ai pas encore répondu à la question de @Pixelax - du moins, je n'ai pas encore regardé le détail!
Bon, et avec tout ça, j'ai pas encore répondu à la question de @Pixelax - du moins, je n'ai pas encore regardé le détail!
Pixelax a écrit:[Dans le cadre du jeu "The Wall",] quelle est la probabilité qu'une boule lâchée au centre tombe dans une case paire (donc à gros gain)?

bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
Boyards : 1275
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
bibi6 a écrit:Et sinon, si ça intéresse quelqu'un, j'ai passé l'écrit de l'agrégation externe spécial hier. Neuf exercices variés, et deux problèmes dont un seul était à choisir et à traiter. Celui que j'ai choisi concernait les principes d'incertitude sur un groupe abélien fini (et le lien est la mécanique quantique); l'autre était sur les mesures cristallines (voir "Espace de Schwartz").
Bon, et avec tout ça, j'ai pas encore répondu à la question de @Pixelax - du moins, je n'ai pas encore regardé le détail!Pixelax a écrit:[Dans le cadre du jeu "The Wall",] quelle est la probabilité qu'une boule lâchée au centre tombe dans une case paire (donc à gros gain)?
Ahhhhh, le concours docteurs ?

Chris K. is watching you, avec modération bien sûr ^^

Julien- Fan-Accro

- Inscription : 03/12/2011
Messages : 2224
Boyards : 3676
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
@Lumiere_du_fort : comme je l'ai déjà dit plus haut, le but de ce sujet n'est pas de poster des excercices scolaires... et encore moins d'en poster 11 d'un coup, en plus sans jamais y revenir ! À la rigueur quand c'est comme ça, il vaut mieux que tu n'en sélectionnes qu'un seul que tu trouves vraiment (mais vraiment) intéressant, et pas que ce soit un problème artificiel qui n'a été créé que dans le but de faire faire des maths à des lycéeens (comme le 7 ou le 9 par exemple).
 ).
).
En fait c'est vrai quelque soit le nombre de trappes en fait, pourvu que le mur soit juste à la bonne hauteur pour que l'on atteigne une trappe extrême si et seulement si on est toujours tombé du même côté.
De manière générale, on veut donc montrer que
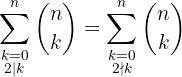
Pour n impair c'est très facile, ça provient directement de la symétrie des coefficients binomiaux. Manque de pot, ici 14 c'est pair !
Pourtant, le résultat tombe en une ligne si on utilise une formule bien pratique qui fait intervenir des coefficients binomiaux...
C'est bien 1/2 en effet, et la démonstration est laaaaaargement en dessous du niveau de l'agrégation spéciale (heureusement que l'épreuve ne portait pas sur la planche de Galtonbibi6 a écrit:Sur le coup, j'aurais dit 1/2, mais je me rends compte en postant que mon argument est bancal. Je réfléchis et je reviensPixelax a écrit:Avant de passer au cas général (où la boule n'est pas forcément lâchée en 4), j'ai une autre petite question pour vous : quelle est la probabilité de tomber dans une trappe impaire (i.e. une grosse somme) ? Comment montrer ce résultat sans utiliser d'application numérique ?
Je rappelle en passant que ça peut être dangereux d'additionner des valeurs approchées car les erreurs peuvent s'accumuler... #JDCJDR
En fait c'est vrai quelque soit le nombre de trappes en fait, pourvu que le mur soit juste à la bonne hauteur pour que l'on atteigne une trappe extrême si et seulement si on est toujours tombé du même côté.
De manière générale, on veut donc montrer que
Pour n impair c'est très facile, ça provient directement de la symétrie des coefficients binomiaux. Manque de pot, ici 14 c'est pair !
Pourtant, le résultat tombe en une ligne si on utilise une formule bien pratique qui fait intervenir des coefficients binomiaux...

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Oui, je devais revenir, et je suis pas revenu... 
Mais j'ai, je pense, l'argument "qui va bien". Mais je laisse les autres réfléchir
[HS]Et concernant les concours, l'agrég "externe spécial" est bien pour les docteurs, et j'ai été voir le CAPES ces deux derniers jours. Et j'ai bien gratté du papier
En résumé, hier: Option info, sudoku et géométrie algorithmique; option math, réseaux et pavages du plan, et involutions sur les réels positifs. Aujourd'hui, pour tous: méthode de Monte-Carlo pour le quart de cercle et PageRank.[/HS]
Mais j'ai, je pense, l'argument "qui va bien". Mais je laisse les autres réfléchir
[HS]Et concernant les concours, l'agrég "externe spécial" est bien pour les docteurs, et j'ai été voir le CAPES ces deux derniers jours. Et j'ai bien gratté du papier
En résumé, hier: Option info, sudoku et géométrie algorithmique; option math, réseaux et pavages du plan, et involutions sur les réels positifs. Aujourd'hui, pour tous: méthode de Monte-Carlo pour le quart de cercle et PageRank.[/HS]

bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
Boyards : 1275
Page 7 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8 
Page 7 sur 8
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Accueil
Accueil S'enregistrer
S'enregistrer Connexion
Connexion