Coin MATHÉMATIQUES
+11
Carlobservateur
Bastien
Julien
Paul
Peyo13
Anonyme
bibi6
rhyolite
RiverOfBoyards
garsim
Pix
15 participants
Page 5 sur 8
Page 5 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8 
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
a)
Donc 6 essais, pour un gain moyen de 46 + 2/3 (moi dire 46,67 environ ça me convient, mais comme mÔssieu aime les valeurs exactes  ) !
) !
| Gain | Gain moyen | |
| 1 | 10 | 8,888888889 |
| 2 | 25 | 19,44444444 |
| 3 | 45 | 30 |
| 4 | 70 | 38,88888889 |
| 5 | 100 | 44,44444444 |
| 6 | 140 | 46,66666667 |
| 7 | 190 | 42,22222222 |
| 8 | 250 | 27,77777778 |
garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
En effet, mÔssieur aime l'exactitude (ceci dit des valeurs approchées c'est bien aussi parfois, tant qu'on précise que c'en sont ^^), mais mÔssieur préfère voir de jolies courbes plutôt que de devoir regarder dans les yeux un tableau de nombres tout mochegarsim a écrit:Donc 6 essais, pour un gain moyen de 46 + 2/3 (moi dire 46,67 environ ça me convient, mais comme mÔssieu aime les valeurs exactes) !

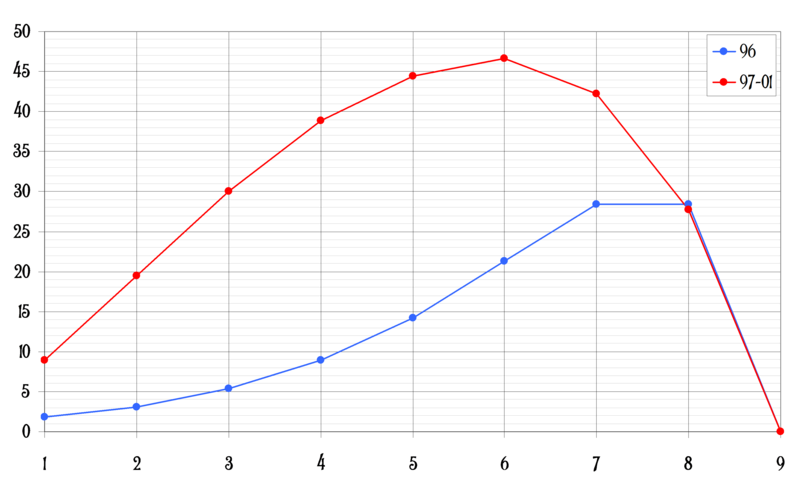
Gain moyen en fonction du nombre de boyards retournés
La maximum est atteint en 6, c'est donc une bonne réponse ! Je rappelle que si xk désigne le gain en cas de succès après la kème pièce (pour l'échelle 96, xk = 2k pour k ⩽ 8), le gain moyen est de xk(9-k)/9. Pour k=6, on trouve en effet 46 + 2/3.
En tout cas, une chose est claire : l'échelle 97-01 est bien plus avantageuse pour le candidat que celle de 96..!
Pour la b) pas la peine de me faire un graphique puisque c'est ça qui est imposé : tous les points (à l'exception du dernier bien sûr, qui lui ne pourra jamais décoller de 0) doivent être alignés horizontalement.

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
b) En fait, pour peu qu'on ait résolu le problème précédent, c'est pas très difficile vu qu'on fixe le gain maximum à 250 ^^
Donc pour 8 essais, le gain et le gain moyen ne changent pas, il reste égal à 250/9.
Pour les autres, on prend la formule du gain moyen :
On remplace les valeurs qu'on connaît, entre autres Gm qui ne dépend plus de k vu qu'il est désormais constant :
Ce qui donne une choulie équation paramétrée dont xk est l'inconnue et k le paramètre.
En faisant varier k entre 1 et 7, on peut remplir le reste du tableau.
Donc pour 8 essais, le gain et le gain moyen ne changent pas, il reste égal à 250/9.
Pour les autres, on prend la formule du gain moyen :
Gmk = xkP(k)
On remplace les valeurs qu'on connaît, entre autres Gm qui ne dépend plus de k vu qu'il est désormais constant :
250/9 = xk(9-k)/9
Ce qui donne une choulie équation paramétrée dont xk est l'inconnue et k le paramètre.
En faisant varier k entre 1 et 7, on peut remplir le reste du tableau.
| Gain (val. exacte) | Gain (val. approx) | |
| 1 | 31,25 | 31,25 |
| 2 | 250/7 | 35,71 |
| 3 | 125/3 | 41,67 |
| 4 | 50 | 50 |
| 5 | 62,5 | 62,5 |
| 6 | 750/9 | 83,33 |
| 7 | 125 | 125 |
| 8 | 250 | 250 |

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
garsim a écrit:En faisant varier k entre 1 et 7, on peut remplir le reste du tableau.
Gain
(val. exacte)Gain
(val. approx)1 31,25 31,25 2 250/7 35,71 3 125/3 41,67 4 50 50 5 62,5 62,5 6 750/9 83,33 7 125 125 8 250 250
Ça ressemble fort à une bonne réponse !

Du coup, cette échelle est "neutre" puisqu'à part si on se plante dès le départ, on peut voir chaque étape comme un jeu équitable (c'est-à-dire d'espérance nulle), et ce jusqu'à la huitième pièce.
⁂
Tout autre chose, un autre petit problème mathématique plus ou moins boyardesque, mais qui n'a rien à voir avec des probas soulagé ?. Encore mieux, il ne nécessite aucune connaissance en maths, tout le monde peut répondre
Il y a presque 3 ans, @Thibault avait posté une idée de duel :
Thibault a écrit:La Chenille :
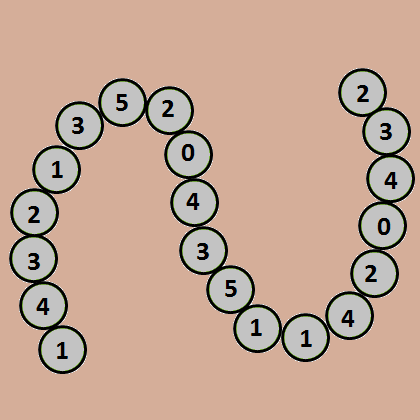
Sur la table, il y a 20 petites pièces en bois (ou 16, 18, 22 mais il faut un nombre pair). Elles sont placées les unes à la suite des autres et sur chacune d'elle il y a un chiffre (Par exemple de 0 à 5)
A tour de rôle, le candidat et le maître vont devoir prendre une pièce. Mais pas n'importe laquelle !! Uniquement une des deux qui sont situées aux extrémités.
A la fin, le père Fouras additionne les chiffres de chacun : celui qui a le plus grand nombre remporte le duel !
Donc requiert beaucoup de stratégie ^^
Ca pourrait ressembler à ça :
Vous voyez ma question venir à 10km (si ce n'est pas le cas c'est que vous ne me connaissez pas assez
Bon OK, je reformule ça correctement : Quelle stratégie faut-il adopter pour gagner à tous les coups ? En particulier, faut-il commencer ou laisser la main à l'adversaire ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Oui, parce que bon, sinon c'est pas très gentil pour celui qui a proposé le duel...Pixelax a écrit:Pourquoi ce duel est-il TOUT POURRI ?
Bon OK, je reformule ça correctement : Quelle stratégie faut-il adopter pour gagner à tous les coups ? En particulier, faut-il commencer ou laisser la main à l'adversaire ?
Ah, un peu d'algorithmique
Alors, je propose déjà de dissocier deux cas de figure :
- Si le nombre d'éléments dans la chenille est pair, il faut toujours prendre la main.
- Si le nombre d'éléments dans la chenille est impair :
- Si la somme des éléments "impairs" de la chenille est supérieure à la somme des éléments "pairs", il faut prendre la main.
- Si la somme des éléments "impairs" de la chenille est inférieure à la somme des éléments "pairs", il faut laisser la main.
- Si ces sommes sont égales, ça va finir en égalité donc osef.
Ensuite, on somme les éléments "pairs" de la chenille ainsi que les "impairs". Si la somme des "pairs" est supérieure, il faut prendre l'élément à l'extrémité droite. Sinon, il faut prendre celui à l'extrémité gauche.
(si le nombre d'éléments à votre disposition est impair, peu importe en principe, par défaut prenez le plus grand des deux)
Cette stratégie me semble logique : à plus petite échelle (3 ou 4 éléments), ça peut se vérifier sur des cas simples :
- Pour une chenille de 3 chiffres a b c : si a + c > b, il est évident qu'il faut commencer pour être gagnant ! Prendre max(a, c) ; quel que soit le chiffre restant que l'autre joueur prendra, il sera inférieur à la somme des deux chiffres que vous aurez pu prendre. En revanche, si a + c > b, il faut laisser la main, car si on commence, on devra prendre une valeur qui va libérer le b pour l'adversaire, qui aura gagné vu que b > a + c...
- Pour une chenille de 4 chiffres a b c d : c'est un peu plus délicat. Par exemple, si on se retrouve avec 1 3 9 2, il est évident que c'est celui qui aura réussi à avoir le 9 qui va gagner. Si je commence, je vais avoir le choix entre 1 et 2. Mais en choisissant 2, je laisse un boulevard à l'autre joueur qui va alors se précipiter sur le 9, et je vais perdre d'avance ! Alors que si je prends le 1, l'autre joueur n'aura pas le choix et devra prendre un chiffre qui libèrera le 9 que je pourrai alors prendre.
En se ramenant à ces deux cas de figure, puis en procédant par récursivité, on peut s'en sortir pour des chenilles plus grande.
Pour les cas de figure que j'ai pu tester, en tout cas, ça marche.
En bonus track, si vous avez un compilateur C++ sous la main, voici le code d'un petit programme console entre deux "joueurs" artificiels :
- Code:
#include <iostream>
#include <fstream>
#include <deque>
#include <cstdlib>
#include <ctime>
#define PAUSE_APRES_COUP
using namespace std;
enum Tour_jeu {j1 = 0, j2 = 1}; // Tour de jeu : 0 => joueur 1 ; 1 => joueur 2
/*
* Retourne un nombre au hasard entre a et b
* a : borne supérieure
* b : borne inférieure
* return Nombre aléatoire
*/
int rand_a_b(int a, int b)
{
return rand() % (b - a) + a;
}
class Partie
{
public:
/*
* Constructeur
*/
Partie()
{
score[j1] = 0;
score[j2] = 0;
}
/*
* Determine qui va commencer
* return Qui commence
*/
Tour_jeu qui_commence()
{
// Cas 1 : le tableau est de taille impaire
if((taille_tableau % 2) == 1)
{
// Cas 1a) : la somme des éléments pairs est supérieure à la somme des éléments impairs
// Dans ce cas, on commence
// Cas 1b) : la somme des éléments pairs est inférieure à la somme des éléments impairs
// Dans ce cas, on laisse l'adversaire commencer
tour_jeu = pairs_superieurs() ? j1 : j2;
}
// Cas 2 : le tableau est de taille paire
// On commence dans tous les cas
else
{
tour_jeu = j1;
}
return tour_jeu;
}
/*
* Lance la partie (fonction récursive jouant un coup à chaque appel)
*/
void jouer_coup()
{
if(taille_tableau > 0)
{
// Affichage des cases restantes
afficher_tableau();
// A qui le tour ?
qui_tour();
// Coup en cas de taille de tableau paire
if((taille_tableau % 2) == 0)
{
choisir_case_paire();
}
// Coup en cas de taille de tableau impaire
else
{
choisir_case_impaire();
}
// Réduction de la taille du tableau
taille_tableau--;
// Affichage des scores
afficher_scores();
// Changement de joueur
tour_jeu = ((tour_jeu == j1) ? j2 : j1);
#ifdef PAUSE_APRES_COUP
getchar(); // Si activé, appuyer sur une touche pour continuer
#endif // PAUSE_APRES_COUP
// Coup suivant
jouer_coup();
}
else
{
cout << "Partie terminee !" << endl;
}
}
/*
* Retourne true si la somme des éléments pairs du tableau est supérieure à la somme des éléments impairs
*/
bool pairs_superieurs()
{
int somme_pairs = 0, somme_impairs = 0;
for(int i = 0 ; i < taille_tableau ; ++i)
{
if((i % 2) == 0)
{
somme_pairs += T[i];
}
else
{
somme_impairs += T[i];
}
}
return (somme_pairs >= somme_impairs);
}
/*
* Détermine la case à prendre lorsque le nombre d'éléments du tableau est pair
* return Contenu de la case choisie
*/
void choisir_case_paire()
{
int case_choisie;
// Si les pairs sont supérieurs, on choisit le premier élément du tableau
if(pairs_superieurs())
{
case_choisie = T.front();
T.pop_front();
}
// Si les impairs sont supérieurs, on choisit le dernier élément du tableau
else
{
case_choisie = T.back();
T.pop_back();
}
// Affichage de la case choisie
cout << "Choix de la case : " << case_choisie << endl;
// Mise à jour des scores
score[tour_jeu] += case_choisie;
}
/*
* Détermine la case à prendre lorsque le nombre d'éléments du tableau est impair
* return Contenu de la case choisie
*/
void choisir_case_impaire()
{
// Par défaut, on va prendre l'élément le plus grand parmi les deux proposés
int case_choisie;
if(T.front() >= T.back())
{
case_choisie = T.front();
T.pop_front();
}
else
{
case_choisie = T.back();
T.pop_back();
}
// Affichage de la case choisie
cout << "Choix de la case : " << case_choisie << endl;
// Mise à jour des scores
score[tour_jeu] += case_choisie;
}
/*
* A qui le tour ?
*/
void qui_tour()
{
if(tour_jeu == j1)
{
cout << "C'est au joueur 1 de jouer." << endl;
}
else
{
cout << "C'est au joueur 2 de jouer." << endl;
}
}
/*
* Retourne le gagnant de la partie
*/
void qui_gagne()
{
if(score[j1] == score[j2])
{
cout << "Egalite !" << endl;
}
else if(score[j1] > score[j2])
{
cout << "Joueur 1 vainqueur !" << endl;
}
else
{
cout << "Joueur 2... vainqueur !? Zut, j'ai du me planter dans mon algo..." << endl;
}
}
/*
* Charge le contenu du tableau à partir d'un fichier
*/
void charger_tableau(char* nom_fichier)
{
ifstream fichier (nom_fichier, ios::in);
int valeur;
if(fichier.is_open())
{
while(!fichier.eof())
{
fichier >> valeur;
T.push_back(valeur);
}
taille_tableau = T.size();
fichier.close();
}
else cerr << "Impossible d'ouvrir le fichier " << nom_fichier << " ; assurez-vous qu'il existe bien." << endl;
}
/*
* Charge le tableau aléatoirement
* taille_tableau : nombre d'éléments du tableau
* borne_min : borne inférieure
* borne_max : borne supérieure
*/
void charger_tableau(int t_tab, int borne_min, int borne_max)
{
taille_tableau = t_tab;
for(int i = 0 ; i < t_tab ; ++i)
{
T.push_back(rand_a_b(borne_min, borne_max));
}
}
/*
* Affichage du tableau
*/
void afficher_tableau()
{
cout << "Tableau en cours : ";
for(int i = 0 ; i < taille_tableau ; ++i)
{
cout << T[i] << " ";
}
cout << endl;
}
/*
* Affichage des scores
*/
void afficher_scores()
{
cout << "Score joueur 1 : " << score[j1] << endl;
cout << "Score joueur 2 : " << score[j2] << endl << endl;
}
private:
/* Tableau de valeurs */
deque<int> T;
/* Taille du tableau */
int taille_tableau;
/* A qui le tour */
Tour_jeu tour_jeu;
/* Scores */
int score[2];
};
/*
* Lancement du jeu
* Mettre en paramètre le nom du fichier contenant la séquence de jeu
* Si pas de paramètre, la séquence sera générée aléatoirement
*/
int main(int argc, char** argv)
{
Partie p;
int taille_tableau, borne_min, borne_max;
if(argc == 1)
{
cout << "Taille du tableau : ";
cin >> taille_tableau;
cout << "Borne min : ";
cin >> borne_min;
cout << "Borne max : ";
cin >> borne_max;
srand(time(NULL));
p.charger_tableau(taille_tableau, borne_min, borne_max);
}
else
{
p.charger_tableau(argv[1]);
}
p.afficher_tableau();
if(p.qui_commence() == j1)
{
cout <<"Joueur 1 prend la main" << endl << endl;
}
else
{
cout <<"Joueur 1 laisse Joueur 2 commencer" << endl << endl;
}
#ifdef PAUSE_APRES_COUP
getchar(); // Si activé, appuyer sur une touche pour continuer
#endif // PAUSE_APRES_COUP
p.jouer_coup();
p.qui_gagne();
return 0;
}
C'est au passage un très bon exemple de l'utilisation du conteneur deque, qui est en fait une file "aux deux extrémités", optimisée pour ajouter/supprimer le premier et le dernier élément. Ce qu'on fait dans cette idée de duel de la Chenille, vu que les joueurs ne peuvent prendre que les éléments situés aux extrémités
PS : vous étonnez pas si, dans le code source, j'ai interverti "pair" et "impair" par rapport à mes explications, mais c'est juste qu'en informatique, les tableaux démarrent à l'indice 0 et pas à 1...
(mouahaha, l'informaticien a parasité le coin mathématiques !

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Alors pour le cas pair c'est une bonne réponse !  À vrai dire j'en attendais pas plus.
À vrai dire j'en attendais pas plus.
En revanche, ce que tu proposes pour le cas impair de marche pas (même si on suppose que tous les points sur les pièces sont positifs), je te laisse trouver un contre-exemple
 Oui ici c'est le coin maths, la récursivité c'est pour le coin informatique
Oui ici c'est le coin maths, la récursivité c'est pour le coin informatique 
 À vrai dire j'en attendais pas plus.
À vrai dire j'en attendais pas plus.En revanche, ce que tu proposes pour le cas impair de marche pas (même si on suppose que tous les points sur les pièces sont positifs), je te laisse trouver un contre-exemple
Depuis quand on ne fait que l'initialisation pour une récurrence ?garsim a écrit:Pour une chenille de 3 chiffres a b c : si a + c > b, il est évident qu'il faut commencer pour être gagnant !
[...] en procédant par récursivité, on peut s'en sortir pour des chenilles plus grande.
 Oui ici c'est le coin maths, la récursivité c'est pour le coin informatique
Oui ici c'est le coin maths, la récursivité c'est pour le coin informatique 

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
En fait, j'avais tout simplement zappé que dans la description du duel, il était précisé que le nombre d'éléments était pair !Pixelax a écrit:Alors pour le cas pair c'est une bonne réponse ! À vrai dire j'en attendais pas plus.
J'aurais dû relire le post en entier pour m'épargner une réflexion supplémentaire inutile !
Pour le cas de trois éléments, ça ne change pas par rapport à ce que j'ai dit ci-dessus : j'ai tout intérêt à commencer si le chiffre du centre est inférieur à ceux des extrémités.Pixelax a écrit:En revanche, ce que tu proposes pour le cas impair de marche pas (même si on suppose que tous les points sur les pièces sont positifs)
Pour le cas où la somme des éléments pairs est égale à celle des éléments impairs, ça débouche quand même sur une égalité, comme on a pu en discuter hier sur la CB (je te laisse remettre la démonstration si tu as sauvegardé cette archive-là ^^).
Pour les autres cas, en revanche, effectivement la stratégie que j'ai décrite plus haut ne marche pas à tous les coups.
Contre-exemple : 1 2 5 1 2. On a bien 1 + 5 + 2 > 2 + 1 ; pourtant, si je commence, je me fais avoir dans tous les cas, vu que si je prends le 2 et que l'adversaire prend le 1 à gauche, il va me forcer à libérer le 5 dont il va s'emparer. Ce qui me ferait alors 2 + 2 + 1 = 5 contre 1 + 5 = 6 pour lui.
Supposons un cas généralisé type c a1 b1 a2 b2 ... an-1 bn-1 an d.
Si je commence et que je prends d (si je prends c, on peut se ramener au même cas en permutant c et d), on se ramène à un cas pair :
c a1 b1 a2 b2 ... an-1 bn-1 an
On suppose que l'adversaire connaît bien sûr la stratégie gagnante en cas de séquence paire. Dans ce cas, il est gagnant dans les deux cas de figure suivants :
- c + Σbi > Σaj + d : dans ce cas-là, il doit prendre c pour gagner ;
- c + Σbi + d < Σaj : dans ce cas-là, il doit prendre an pour gagner.
Et j'ai donc tout intérêt à lui laisser la main si je veux gagner.
En revanche, si on n'est pas dans ces cas de figure-là, j'ai l'impression que si je commence, je pourrai toujours définir une stratégie gagnante (sauf cas d'égalité dont on a déjà parlé), en prenant max(c, d) et en ramenant l'adversaire au cas pair, qu'il saura résoudre en prenant le meilleur résultat possible de la séquence restante. Mais comme j'aurai additionné d à mon sous-total, ça devrait me permettre de le devancer, vu qu'on a supposé qu'on n'était pas dans les cas de figure perdants décrits ci-dessus, donc que c + Σbi <= Σaj + d ou que c + Σbi + d >= Σaj.
Si cette stratégie est validée, je mettrai mon code source à jour pour l'y intégrer.
C'est nouveau, ça vient de sortir.Pixelax a écrit:Depuis quand on ne fait que l'initialisation pour une récurrence ?
Mais tu ne connais peut-être pas les maths modernes. Quand tu manipules des concepts compliqués, tu en as besoin !

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Moui, on pourrait reformuler ça plus clairement et en ajoutant des précisions mais en gros c'est la bonne réponse ! 


Reprenons. Déjà, je trouve que c'est mieux de noter d le plus grand des deux entre c et d quitte à les permuter, plutôt que d'en fixer un selon ce que prend le premier joueur. On a donc c ⩽ d.
Je vais également noter A = Σaj et B = Σbi, ce sera plus simple.
Lorsqu'il y a égalité entre les deux joueurs, je considère que les deux ont gagné.
Si le joueur 1 prend c, le joueur 2 va prendre max(A,B+d). Il restera alors min(A,B+d) pour le joueur 1, en plus du c qu'il a déjà.
Donc dans ce cas, le joueur 1 gagne ssi max(A,B+d) ⩽ min(A,B+d) + c
ssi |B+d-A| ⩽ c
ssi |d-δ| ⩽ c, en posant δ = A-B
ssi δ ∈ [d ± c] (1) (je rappelle que [x ± y] est une notation pour l'intervalle [x-y ; x+y], qu'on considère comme vide si y<0)
De même, si le joueur 1 commence par d, il gagne ssi δ ∈ [c ± d] (2)
Dans le cas général, on a donc le joueur 1 gagne ssi (1) OU (2).
Or, comme c ⩽ d, (1)⇒(2). Cela veut donc dire que si le joueur 1 peut gagner en prenant c, il le peut aussi en prenant d. Il a donc tont intérêt à prendre systématiquement d (càd la plus grande des deux), comme tu l'as dit.
On a finalement la caractérisation suivante : le joueur 1 gagne ssi δ ∈ [c ± d]
En reprenant la preuve, on se rend compte que de plus on a égalité entre les deux joueurs ssi on est au bord de l'intervalle, i.e δ ∈ {c ± d}.
Quelques exemples :
Remarque : on utilise nulle part que les points sur les pièces sont positifs en fait, ce qu'on a fait reste vrai dans le cas général. En outre, on remarque que si d<0 (donc c aussi par hypothèse), le joueur 1 a perdu quelques soient les autres pièces !

En tout cas merci @Thibault pour nous avoir proposé ce jeu qui nous aura bien occupé (ce n'est rien d'autre qu'un problème de maths hein, pas un duel du Conseil ^^)

"J'ai l'impression que [...]" n'est pas un argument très convaincantgarsim a écrit:En revanche, si on n'est pas dans ces cas de figure-là, j'ai l'impression que si je commence, je pourrai toujours définir une stratégie gagnante [...] en prenant max(c, d)
Attention M. le logicien, on n'est dans aucun des deux cas de figure donc on est dans la négation du premier ET la négation du deuxièmegarsim a écrit:[...] vu qu'on a supposé qu'on n'était pas dans les cas de figure perdants décrits ci-dessus, donc que c + Σbi <= Σaj + d ou que c + Σbi + d >= Σaj.
Reprenons. Déjà, je trouve que c'est mieux de noter d le plus grand des deux entre c et d quitte à les permuter, plutôt que d'en fixer un selon ce que prend le premier joueur. On a donc c ⩽ d.
Je vais également noter A = Σaj et B = Σbi, ce sera plus simple.
Lorsqu'il y a égalité entre les deux joueurs, je considère que les deux ont gagné.
Si le joueur 1 prend c, le joueur 2 va prendre max(A,B+d). Il restera alors min(A,B+d) pour le joueur 1, en plus du c qu'il a déjà.
Donc dans ce cas, le joueur 1 gagne ssi max(A,B+d) ⩽ min(A,B+d) + c
ssi |B+d-A| ⩽ c
ssi |d-δ| ⩽ c, en posant δ = A-B
ssi δ ∈ [d ± c] (1) (je rappelle que [x ± y] est une notation pour l'intervalle [x-y ; x+y], qu'on considère comme vide si y<0)
De même, si le joueur 1 commence par d, il gagne ssi δ ∈ [c ± d] (2)
Dans le cas général, on a donc le joueur 1 gagne ssi (1) OU (2).
Or, comme c ⩽ d, (1)⇒(2). Cela veut donc dire que si le joueur 1 peut gagner en prenant c, il le peut aussi en prenant d. Il a donc tont intérêt à prendre systématiquement d (càd la plus grande des deux), comme tu l'as dit.
On a finalement la caractérisation suivante : le joueur 1 gagne ssi δ ∈ [c ± d]
En reprenant la preuve, on se rend compte que de plus on a égalité entre les deux joueurs ssi on est au bord de l'intervalle, i.e δ ∈ {c ± d}.
Quelques exemples :
| Chenille | δ | [c ± d] | Gagnant |
| 2 3 10 5 3 | -2 | [-1 ; 5] | Joueur 2 |
| 2 3 9 5 3 | -1 | [-1 ; 5] | Égalité |
| 2 3 8 5 3 | 0 | [-1 ; 5] | Joueur 1 |
| 2 3 5 5 3 | 3 | [-1 ; 5] | Joueur 1 |
| 2 3 3 5 3 | 5 | [-1 ; 5] | Égalité |
| 2 3 2 5 3 | 6 | [-1 ; 5] | Joueur 2 |
Remarque : on utilise nulle part que les points sur les pièces sont positifs en fait, ce qu'on a fait reste vrai dans le cas général. En outre, on remarque que si d<0 (donc c aussi par hypothèse), le joueur 1 a perdu quelques soient les autres pièces !
Meuh non c'était pas inutile c'était très intéressant, et puis ça change des probas tu vas pas te plaindre ! ^^ mais je jure que je n'avais pas prévu de poser la questiongarsim a écrit:En fait, j'avais tout simplement zappé que dans la description du duel, il était précisé que le nombre d'éléments était pair !
J'aurais dû relire le post en entier pour m'épargner une réflexion supplémentaire inutile !
En tout cas merci @Thibault pour nous avoir proposé ce jeu qui nous aura bien occupé (ce n'est rien d'autre qu'un problème de maths hein, pas un duel du Conseil ^^)

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Allez, on va essayer de convaincre @Paul et @Quentin 
Un petit problème virtuel-boyardesque. Dans l'épreuve du C+ C-, le candidat doit deviner un nombre entier entre 0 et 100 préalablement choisi par l'animateur. Il a le droit à 6 essais, et pour chacun d'eux l'animateur lui annonce si le nombre recherché est strictement supérieur au nombre annoncé (C'EST PLUS !), strictement inférieur (C'EST MOINS !) ou égal (C'EST GAGNÉ !!!). Le candidat gagne ssi une de ses 6 propositions est égale au nombre recherché.
Quelle est la stratégie optimale ? Quelle est alors la probabilité de succès ? Et surtout, pourquoi est-il impossible de faire mieux ?
Plus généralement, si l'entier recherché est entre 0 et M, quelle valeur ne doit pas excéder M pour gagner à coup sûr avec n essais ?
Un petit problème virtuel-boyardesque. Dans l'épreuve du C+ C-, le candidat doit deviner un nombre entier entre 0 et 100 préalablement choisi par l'animateur. Il a le droit à 6 essais, et pour chacun d'eux l'animateur lui annonce si le nombre recherché est strictement supérieur au nombre annoncé (C'EST PLUS !), strictement inférieur (C'EST MOINS !) ou égal (C'EST GAGNÉ !!!). Le candidat gagne ssi une de ses 6 propositions est égale au nombre recherché.
Quelle est la stratégie optimale ? Quelle est alors la probabilité de succès ? Et surtout, pourquoi est-il impossible de faire mieux ?
Plus généralement, si l'entier recherché est entre 0 et M, quelle valeur ne doit pas excéder M pour gagner à coup sûr avec n essais ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Tu veux que ce soient eux qui répondent, ou bien... ? Parce que moi, je veux bien dire en quoi cette épreuve est TOUTE POURRIE (ben quoi, toi-même tu as employé ces termes au sujet d'un duel récemment...
 ).
).Bon, pour résoudre un problème du style "Je pense à un nombre entre x et y", la méthode la plus efficace (sans compter sur la chance), ça reste la dichotomie. A savoir : donner le nombre "pile entre les deux", puis si on nous dit que "c'est moins", on donne le nombre "pile entre x et (x + y)/2" (puis on continue en reprenant l'étape précédente et en remplaçant y par (x + y)/2 ) ; ou si c'est plus, on donne le nombre "pile entre (x + y)/2 et y" (puis on continue en reprenant l'étape précédente et en remplaçant x par (x + y)/2 ). Au bout d'un moment, on arrive forcément à tomber sur le bon nombre.
Algorithmiquement parlant (désolé
 ), si on compare l'algorithme "brut" qui va tester tous les chiffres un par un :
), si on compare l'algorithme "brut" qui va tester tous les chiffres un par un :- Code:
int trouver_nombre_mystere(int min, int max)
{
int i = min;
do
{
if(i == nb_mystere)
{
cout << nb_mystere << " est le bon nombre ! Felicitations !" << endl;
}
else
{
cout << "Vous proposez " << i << " : c'est plus !" << endl;
}
i += 1;
} while(i <= max)
return i;
}
- Code:
int trouver_nombre_mystere(int min, int max)
{
int i = (min + max) / 2;
if(i == nb_mystere)
{
cout << nb_mystere << " est le bon nombre ! Felicitations !" << endl;
return i;
}
else if(i < nb_mystere)
{
cout << "Vous proposez " << i << " : c'est plus !" << endl;
return trouver_nombre_mystere(i, max);
}
else
{
cout << "Vous proposez " << i << " : c'est moins !" << endl;
return trouver_nombre_mystere(min, i);
}
}
Pour voir ça, comparons le nombre maximal d'essais nécessaire n entre la première méthode (par incrémentation) et la seconde (par dichotomie). Je vais revenir aux données du problème en fixant min = 1 et max = M.
NB : oui, je sais que le problème initial partait de min = 0, mais démarrer à min = 1 va considérablement simplifier mes calculs par la suite. Il est de toute façon facile de se reporter au cas min = 0 après ça : par exemple, au lieu de trouver entre 0 et 100, on va trouver entre 1 et 101 puis retrancher 1.
Première méthode : comme vous testez tous les nombres un par un, soit vous avez du pot et il se trouve dans les premiers, soit vous n'avez pas de bol et il se trouve dans les derniers. Pis, si c'est le dernier, ça veut dire que vous aurez testé tous les nombres avant. Donc nmax = M.
Deuxième méthode : intuitivement, faisons quelques essais sur des échantillons restreints :
- Un nombre entre 1 et 1 : euh, là, si vous le trouvez pas du premier coup, c'est que vous êtes grave. nmax = 1, si vous proposez autre chose, soit vous êtes un troll, soit je vais beaucoup m'inquiéter concernant vos capacités de réflexion.

- Un nombre entre 1 et 2 : bon, là, vous êtes d'accord que, si vous en proposez un et que ce n'est pas le bon, c'est forcément l'autre !
 Donc nmax = 2.
Donc nmax = 2. - Un nombre entre 1 et 3 : ici, commencez par dire le "nombre du milieu", càd 2. Si on vous dit que c'est moins, ce sera forcément 1 ; si c'est plus, ce sera forcément 3. Dans les deux cas, nmax = 2 là encore.
- Un nombre entre 1 et 4 : là, en revanche, ça se corse. Prenons 2 par exemple : si on vous dit que c'est plus, cette fois-ci, on a deux possibilités (3 et 4), donc nmax = 3. Si vous commencez par 3, le problème sera le même si on vous dit que c'est moins.
- Un nombre entre 1 et 5 : pas de changement par rapport au problème précédent, si vous commencez par 3, vous aurez toujours nmax = 3.
- ...
- Un nombre entre 1 et 7 : dernier intervalle où nmax = 3. Cette fois, vous pouvez commencer par 4 : si c'est moins, vous faites 2 puis vous tomberez de toute façon sur 3 essais au maximum ; si c'est plus, vous proposez ensuite 6, et il ne restera au pire que 5 ou 7.
- Un nombre entre 1 et 8 : là, en revanche, dans le pire des cas, il vous faudra nmax = 4 essais pour être sûr de parvenir à trouver le bon nombre. Si, par exemple, vous démarrez à 4, que "c'est plus", puis que vous proposez 6 et que "c'est plus" : il restera alors 7 ou 8 à tester, et si vous testez le "mauvais" en premier, vous aurez alors eu besoin de 4 essais.
Penchons-nous sur ce dernier cas : en fait, vous avez remarqué que, une fois qu'on a pris notre première tentative et qu'on a su vers où aller, on pouvait déterminer le nombre maximal d'essais qu'il nous restait à faire ? En effet, si c'est moins que 3, on retombe sur {1; 2; 3} à tester (ce qu'on sait déjà faire, cf. quelques lignes plus haut) ; et si c'est plus, on a {5; 6; 7; 8}, qui se rapporte au même cas que {1; 2; 3; 4} qu'on a aussi déjà vu !
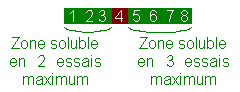
Il suffit donc, pour obtenir notre nmax, de prendre le nmax - 1 des deux cas de part et d'autre de notre valeur "pivot", et d'ajouter 1.
En fait, on peut généraliser comme suit un ensemble de valeurs soluble en maximum n tentatives :
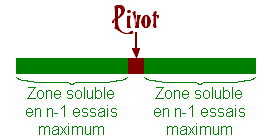
Bref, une récurrence, quoi ^^
Si on prend n-1 de part et d'autre de la valeur pivot, on est d'ailleurs dans le cas où on a trouvé le Mmax le plus grand pour un nombre d'essais n donné.
Exemple :

Pour formaliser notre problème, je vais définir la suite de valeurs (Mn) comme étant la suite des plus grandes valeurs de M possibles soluble en maximum n essais.
On a déjà quelques valeurs de M pour certains n donnés (cf. explications et schémas ci-dessus) :
- M0 = 0 (ben oui, si vous n'avez pas de chiffre à deviner, vous ne pouvez rien proposer, c'est logique
 )
) - M1 = 1 (il n'y a qu'entre 1 et... 1 qu'on peut être sûr à 100% de trouver en un seul essai)
- M2 = 3 (cf. schéma précédent)
- M3 = 7 (idem)
- M4 = 15
Plus généralement, comme je viens de dire que la suite était définie par récurrence, c'est qu'on peut déduire Mn+1 à partir de Mn. Ici, en l'occurrence, Mn+1 = 2Mn + 1.
Bref, une bête suite arithmético-géométrique, dont on peut déduire le terme général : Mn = 2n - 1 (je vous épargne le détail des calculs car j'ai pas envie de faire du LaTeX là
Revenons à nos moutons.
Dans l'épreuve du "C+ C-", nous devons trouver un nombre entre 1 et 101 (ça revient au même qu'entre 0 et 100, on a juste décalé d'un cran pour simplifier nos calculs), et n'avons donc droit qu'à 6 essais maximum. Donc n = 6, et il faut qu'on croise les doigts pour que M6 >= 101.
Si on reprend notre formule, M6 = 26 - 1 = 64 - 1 = 63.
Et *Ristar*, ça ne marche pas !!!
Notez qu'au passage, avec une tentative de plus, comme M7 = 127, vous auriez pu gagner à tous les coups ; ce qui aurait donc transformé cette épreuve de chance en une épreuve "arnaque" à l'instar des duels des Bâtonnets ou de la Chenille. A vous de voir si vous trouvez que c'est mieux ou non...
Bon, ben, du coup, faute de grives, on plombe des merles...
Pour tenter de limiter la casse, focalisez-vous sur un intervalle, par exemple [1; 63], puis commencez par proposer la valeur pivot de cette intervalle, par exemple 32. Si c'est plus, proposez nque vous venez de proposer + (nque vous venez de proposer / 2) (48 dans l'exemple) ; si c'est moins, nque vous venez de proposer - (nque vous venez de proposer / 2) (16 dans l'exemple), et continuez avec la méthode par dichotomie.
Comme, en 6 tentatives, on ne peut brosser qu'un éventail de 63 valeurs au maximum sur les 101 possibles, la probabilité de réussite est donc de P = 63/101 = 62,37 % environ.
PS : vous aurez constaté que j'ai répondu aux questions de @Pixelax dans le désordre, mais je m'en fiche,

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Si ça te fait plaisir ! ^^ Mais c'est un peu exagéré de dire que ça va considérablement simplifier tes calculs, tu auras juste un "-1" eu lieu d'un "-2"garsim a écrit:NB : oui, je sais que le problème initial partait de min = 0, mais démarrer à min = 1 va considérablement simplifier mes calculs par la suite.
Ahhh en fait c'était pour faire apparaître exactement les nombres de Mersenne ! Bon cette théorie ne sert absolument à rien ici mais pourquoi pasgarsim a écrit:Mn+1 = 2Mn + 1. Bref, une bête suite arithmético-géométrique, dont on peut déduire le terme général : Mn = 2n - 1
Sinon, pour avoir l'expression explicite ici, l'excuse "j'ai pas envie de faire du LaTeX" ne tient pas ici puisque c'est un cas très simple, on peut intuiter la réponse et la prouver en deux lignes juste par une récurrence !
Bref, en tout cas la stratégie que tu exposes est bien celle que j'attendais, c'est une bonne réponse !

Tatata, j'ai bien compris que tu as fait ça juste pour essayer de m'enfumer. Mais tu crois que je ne t'ai pas vu venir ? Il manque la réponse à la question la plus importante !garsim a écrit:vous aurez constaté que j'ai répondu aux questions de @Pixelax dans le désordre, mais je m'en fiche
Pixelax a écrit:Et surtout, pourquoi est-il impossible de faire mieux ?
Je suis censé te croire sur parole ?garsim a écrit:Bon, pour résoudre un problème du style "Je pense à un nombre entre x et y", la méthode la plus efficace (sans compter sur la chance), ça reste la dichotomie.

Plus sérieusement, tu as comparé cette méthode avec la méthode on-ne-peut-plus-débile qui est de ne pas écouter l'animateur et de tester toutes les possibilités indépendamment les unes des autres (bon OK on peut faire encore plus débile en proposant toujours le même nombre, mais là "soit vous êtes un troll, soit je vais beaucoup m'inquiéter concernant vos capacités de réflexion"). J'ai envie de dire : heureusement qu'on peut faire mieux que ça !
La vraie question est donc de savoir si on peut élaborer une stratégie, éventuellement non-déterministe, qui aurait une probabilité de succès strictement supérieure à 63/101. Un peu comme fait @Quentin par exemple, on pourrait essayer de faire une espèce de dichotomie approchée sur ⟦0, 100⟧, en essayant de couper à 40-60 par exemple plutôt que 50-50 et espérer qu'on élimine plus de la moitié des cas à chaque fois... quitte à essayer au hasard si l'intervalle restant est trop grand.
Cette question peut paraître très difficile de prime abord, mais il y a juste besoin d'un petit argument pour conclure. Pas besoin de se lancer des raisonnements tordus de probas. En fait, il n'y a même pas besoin de faire des probas si ça peut en rassurer certain.
Tous les calculs ont déjà été faits, il suffit de voir le problème sous un certain angle pour bien comprendre ce qu'il se passe...

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Ben oui, c'est tellement plus joli les nombres de Mersenne par rapport à ces infâmes "-2"...Pixelax a écrit:Si ça te fait plaisir ! ^^ Mais c'est un peu exagéré de dire que ça va considérablement simplifier tes calculs, tu auras juste un "-1" eu lieu d'un "-2"garsim a écrit:NB : oui, je sais que le problème initial partait de min = 0, mais démarrer à min = 1 va considérablement simplifier mes calculs par la suite.
[...]
Ahhh en fait c'était pour faire apparaître exactement les nombres de Mersenne ! Bon cette théorie ne sert absolument à rien ici mais pourquoi pas
(plus sérieusement, j'arrivais pas à retomber sur mes pattes avec mes formules en commençant à zéro, donc je me suis permis cette petite commodité)
Euh, attends, tu voulais carrément que je démontre le terme général d'une suite arithmético-géométrique alors que c'est déjà très bien expliqué sur Wikipédia ?Pixelax a écrit:Sinon, pour avoir l'expression explicite ici, l'excuse "j'ai pas envie de faire du LaTeX" ne tient pas ici puisque c'est un cas très simple, on peut intuiter la réponse et la prouver en deux lignes juste par une récurrence !
Non, même pas.Pixelax a écrit:Tatata, j'ai bien compris que tu as fait ça juste pour essayer de m'enfumer. Mais tu crois que je ne t'ai pas vu venir ? Il manque la réponse à la question la plus importante !garsim a écrit:vous aurez constaté que j'ai répondu aux questions de @Pixelax dans le désordre, mais je m'en ficheHimself a écrit:Et surtout, pourquoi est-il impossible de faire mieux ?
M'enfin je pensais que le fait que la dichotomie était une bonne stratégie coulait de code source à vrai dire...
Oui, bon, ça, c'était plutôt pour un point de vue algorithmique/informatique que j'avais mis cette méthode à titre de comparaison (et que j'avais envie de parler code source et complexité de l'algorithme juste pour t'enquiquinerPixelax a écrit:Plus sérieusement, tu as comparé cette méthode avec la méthode on-ne-peut-plus-débile qui est de ne pas écouter l'animateur et de tester toutes les possibilités indépendamment les unes des autres (bon OK on peut faire encore plus débile en proposant toujours le même nombre, mais là "soit vous êtes un troll, soit je vais beaucoup m'inquiéter concernant vos capacités de réflexion"). J'ai envie de dire : heureusement qu'on peut faire mieux que ça !
Pixelax a écrit:La vraie question est donc de savoir si on peut élaborer une stratégie, éventuellement non-déterministe, qui aurait une probabilité de succès strictement supérieure à 63/101. Un peu comme fait @Quentin par exemple, on pourrait essayer de faire une espèce de dichotomie approchée sur ⟦0, 100⟧, en essayant de couper à 40-60 par exemple plutôt que 50-50 et espérer qu'on élimine plus de la moitié des cas à chaque fois... quitte à essayer au hasard si l'intervalle restant est trop grand.
Cette question peut paraître très difficile de prime abord, mais il y a juste besoin d'un petit argument pour conclure. Pas besoin de se lancer des raisonnements tordus de probas. En fait, il n'y a même pas besoin de faire des probas si ça peut en rassurer certain.
Tous les calculs ont déjà été faits, il suffit de voir le problème sous un certain angle pour bien comprendre ce qu'il se passe...
Bon, effectivement, en ne coupant pas "pile au milieu" à chaque fois, mais plutôt en légèrement décalé (comme le 40/60 au lieu du 50/50), si le nombre mystère se trouve du côté où il reste moins de valeurs, ça limite le nombre de valeurs possibles et permet de continuer par cette espèce de dichotomie, plus ou moins. Si en revanche on est du côté où il y a le plus de valeurs, peut-être proposer quelque chose d'un peu plus proche de la borne et compter un peu sur la chance...

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Non non, ce que je voulais dire c'est qu'il n'y avait pas besoin de cette théorie pour obtenir ce que l'on voulait comme ici on devinait la forme du terme général, mais bon c'est pas bien gravegarsim a écrit:Euh, attends, tu voulais carrément que je démontre le terme général d'une suite arithmético-géométrique alors que c'est déjà très bien expliqué sur Wikipédia ?Pixelax a écrit:Sinon, pour avoir l'expression explicite ici, l'excuse "j'ai pas envie de faire du LaTeX" ne tient pas ici puisque c'est un cas très simple, on peut intuiter la réponse et la prouver en deux lignes juste par une récurrence !
Si ça coulait de source je n'aurais pas posé la question (et surtout tu aurais su me répondre).garsim a écrit:M'enfin je pensais que le fait que la dichotomie était une bonne stratégie coulait de code source à vrai dire...
Justement, le but est de montrer que, même si l'on compte sur la chance, on aura une probabilité plus importante de s'en sortir avec une vraie déchotomie qu'avec une stratégie un peu chaotique à la @Quentin.garsim a écrit:Bon, effectivement, en ne coupant pas "pile au milieu" à chaque fois, mais plutôt en légèrement décalé (comme le 40/60 au lieu du 50/50), si le nombre mystère se trouve du côté où il reste moins de valeurs, ça limite le nombre de valeurs possibles et permet de continuer par cette espèce de dichotomie, plus ou moins. Si en revanche on est du côté où il y a le plus de valeurs, peut-être proposer quelque chose d'un peu plus proche de la borne et compter un peu sur la chance...
Supposons dans un premier temps la stratégie déterministe. Elle est fixée au début de la partie. Le moyen le plus simple de la représenter est sous forme d'arbre (rien à voir avec ceux utilisés en probas ici). On commence par inscrire le nombre que l'on va proposer au départ, qui va constituer la racine de l'arbre. De là on a 3 branches, correspondant aux trois réponses possibles (-, =, +). La branche = s'arrête comme on a gagné (on peut y mettre un marqueur vert par exemple). Pour les deux autres on écrit un autre nombre au bout, et on crée à nouveau 3 ramifications pour chacun d'eux. On itère ce processus jusqu'à avoir traité les 6 essais.
Voici un exemple avec seulement 3 essais, et des nombres arbitrairement choisis :
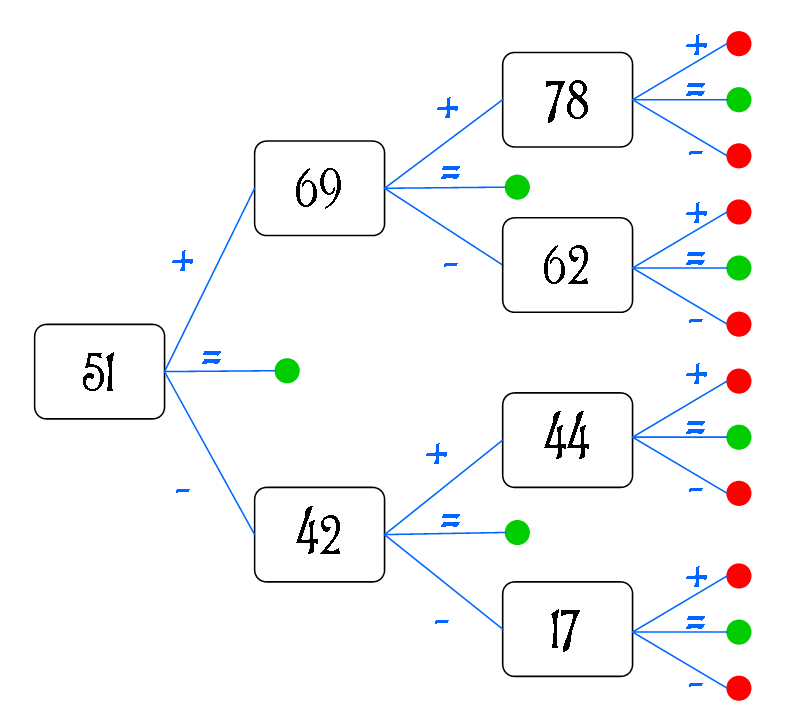
Avec cette représentation, on ne peut gagner que si le nombre recherché est directement relié à un marqueur vert. Il n'y a plus qu'à les compter !
On se rend compte facilement que pour n essais on en a exactement 2n - 1. Quelque soit votre stratégie, il est donc impossible d'identifier strictement plus de 2n - 1 nombres différents. Or, on sait justement que la dichotomie permet d'identifier exactement 2n - 1 nombres. C'est donc la stratégie (déterministe) optimale.
On pourrait croire qu'on a trop simplifié le problème en ne prenant pas en compte les stratégies aléatoires (on pourrait imaginer un arbre plus complexe avec des branches en plus et des probabilités inscrites dessus), mais il n'en est rien. Il suffit d'avoir le bon point de vue ! Vous pouvez très bien décider de faire tous les tirages au sort nécessaires à votre stratégie avant de commencer. On est alors simplement ramené au cas déterministe, où l'on sait que la dichotomie est maître.
Bref, pour en revenir au problème initial, il est impossible d'élaborer une stratégie, même non-déterministe, qui aurait une probabilité de succès strictement supérieure à 63/101. On peut donc résumer cette épreuve à un bête tirage au sort qui aurait une probabilité de succès de 63/101

En d'autre termes, le taux de réussite de cette épreuve ne peut pas, sur le long terme, être beaucoup plus élevé que 63/101 (on pourrait préciser mathématiquement cette phrase mais j'ai pas envie de vous assommer avec des intervalles de fluctuation.... sauf si vous insistez bien sûr !
D'ailleurs, j'en profite pour remettre l'archive du FBV du 12/01 où on m'a bien pris pour un c*n
- Archive 12/01 :
- [22:35:26] @ Paul : C + C -
[22:35:27] @ Paul : Pour Alex
[22:35:47] @ Paul : 6 essais aubout de 5 tu tentes ou tu sors
[22:36:07] @ Paul : si c'est faux prison
[22:36:07] Pixelax : C'est entre 1 et 100 ?
[22:36:11] @ Paul : Entre 0 et 100
[22:37:49] @ Paul : Prêt Alex ?
[22:37:57] Pixelax : oui
[22:38:01] @ Paul : TOP
[22:38:03] Pixelax : 31
[22:38:04] @ Paul : 22 40 01
[22:38:06] @ Paul : PREMIER ESSAI
[22:38:08] @ Paul : PLUS
[22:38:09] @ Paul : 2e essai
[22:38:12] Pixelax : 47
[22:38:15] @ Paul : PLUS
[22:38:17] @ Paul : 3eme essai
[22:38:19] Pixelax : 55
[22:38:22] @ Paul : PLUS
[22:38:23] @ Paul : 4e essai
[22:38:27] Pixelax : 59
[22:38:30] @ Paul : PLUS
[22:38:30] Quentin : belle technique PTDR
[22:38:31] @ Paul : 5e essai
[22:38:36] Pixelax : 61
[22:38:41] @ Paul : PLUS
[22:38:44] @ Paul : il te reste plus qu'un seul essai
[22:38:46] Pixelax : bon bah je sors
[22:38:46] @ Paul : soit tu sors
[22:38:47] Quentin : sors mdrrr
[22:38:47] Pixelax s'est déconnecté le Ven 13 Jan 2017 - 22:38
[22:38:47] @ Paul : soit tu tentes
[22:38:48] Pixelax a rejoint le chat le Ven 13 Jan 2017 - 22:38
[22:38:50] @ Paul : Mais alors là
[22:38:55] Quentin : Mais quest ce que tu as foutu ? XD
[22:38:57] @ Paul : J'ai jamais vu une tel stratégie ^^
[22:38:57] Pixelax : Je pouvais pas faire mieux
[22:39:02] @ Paul : Euh MDRRR
[22:39:06] Pixelax : En fait je gagne ssi ct entre 0 et 62
[22:39:09] Quentin : bah si faire par milieu deja mdr
[22:39:11] garsim : Y a trop peu d'essais pour que la dichotomie soit efficace
[22:39:17] Pixelax : Non mais t'as pas assez d'essais après
[22:39:18] Quentin : bah ca tombe bien cetait 74 ùdr
[22:39:20] Quentin : mdr
[22:39:23] Pixelax : Ben et alors ?
[22:39:33] @ Paul : Nan mais c'est tout à fait faisable aut juste prendre des risques quoi ^ ^
[22:39:35] Pixelax : Je pouvais pas avoir plus de chances de gagner ^^
[22:39:40] Quentin : Bah cetait perdu d'avance mais bon cest pas grave X)
[22:39:40] @ Paul : Si tu joues la moyenne à chaque fois oui t'a aucune chance
[22:39:41] garsim : Faisable, faisable
[22:39:51] garsim : Faut avoir du bol vu l'intervalle et le nombre d'essais oui
[22:39:52] Quentin : bah jai reussi hier
[22:39:54] @ Paul : Totalement faisable tu demanderas à ratman elle à été réussi PLEIN DE FOIS
[22:39:54] Quentin : avant hier ^^
[22:40:01] garsim : T'as eu un saladier avant-hier
[22:40:02] Pixelax : Ben faut du bol
[22:40:09] @ Paul : Non de la méthode ^^
Vous êtes convaincus maintenant ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3645
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je me rappelle de cette épreuve, c'était 97 j'avais réussi et il me restait 0 essai à la fin 

J'ai pas d'idée pour ma signature.

Peyo13- Fan-Illuminé(e)

- Inscription : 26/08/2014
Messages : 545
Boyards : 813
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Pour @Pixelax je suis donc pas convaincu par ce que tu dis puisque c'est pour moi de la stratégie mêlant la chance certes mais de la stratégie où il faut prendre des risques pour avoir une chance 

Paul- Modérateur

- Inscription : 20/08/2010
Messages : 12490
Boyards : 18437
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Paul a écrit:Pour @Pixelax je suis donc pas convaincu par ce que tu dis puisque c'est pour moi de la stratégie mêlant la chance certes mais de la stratégie où il faut prendre des risques pour avoir une chance
Mais JUSTEMENT ! C'est de la stratégie mêlant de la chance, mais certainement pas de la stratégie pure vu qu'on doit nécessairement compter sur la chance pour gagner ! La démonstration qu'on a faite le montre : aucune stratégie ne permet de gagner l'épreuve sans compter sur la chance...
Là, la prise de risques, c'est justement de compter purement et simplement sur la chance : franchement, c'est pas très glorieux pour réussir une épreuve ! Certes, le facteur chance existe pour pas mal d'épreuves (comme les Jarres), mais quand il faut compter uniquement sur lui pour réussir comme pour le C+ C-, ça n'a plus d'intérêt.
La stratégie de @Pixelax lors du FBV et celle de @Quentin basée sur le culot ne diffèrent pas fondamentalement, vu que, dans les deux cas, on a toujours une probabilité de victoire de 63/101...
Certes, Pixelax donne l'impression de brasser un intervalle moins large en se restreignant à l'intervalle [0 ; 63] alors que Quentin qui brasse carrément tout l'intervalle [0 ; 100] ; mais, dans le premier cas, Pixelax est sûr de trouver si le nombre mystère est bien dans l'intervalle [0 ; 63] alors que dans le second on a prouvé que Quentin devait forcément compter sur la chance à un moment ou à un autre. Le truc, c'est surtout que Pixelax compte sur la chance dès le départ en supposant que le nombre mystère est dans un intervalle restreint là où Quentin va aviser au fur et à mesure, mais sans pour autant avoir la garantie de viser juste (comme le montre l'arbre de Pixelax). Et il a beau avoir eu pas mal de chance quand je l'ai mis au défi de trouver les nombres que j'ai tirés au sort avec Excel, il les a quand même pas tous trouvés, donc bon...
Et ne nous parlez pas de "Mais on sait qu'il va prendre un nombre plus près de 0 ou de 100 car il sera plus difficile à cerner dès le départ", car là, ce ne sont plus des mathématiques, mais du mentalisme.

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
Page 5 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8 
Page 5 sur 8
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Accueil
Accueil S'enregistrer
S'enregistrer Connexion
Connexion