Coin MATHÉMATIQUES

Paul a écrit:Pour @Pixelax je suis donc pas convaincu par ce que tu dis puisque c'est pour moi de la stratégie mêlant la chance certes mais de la stratégie où il faut prendre des risques pour avoir une chance

Mais JUSTEMENT ! C'est de la stratégie mêlant de la chance, mais certainement pas de la stratégie pure vu qu'on doit nécessairement compter sur la chance pour gagner ! La démonstration qu'on a faite le montre : aucune stratégie ne permet de gagner l'épreuve sans compter sur la chance...
Là, la prise de risques, c'est justement de compter purement et simplement sur la chance : franchement, c'est pas très glorieux pour réussir une épreuve ! Certes, le facteur chance existe pour pas mal d'épreuves (comme les Jarres), mais quand il faut compter uniquement sur lui pour réussir comme pour le C+ C-, ça n'a plus d'intérêt.

La stratégie de @Pixelax lors du FBV et celle de @Quentin basée sur le culot ne diffèrent pas fondamentalement, vu que, dans les deux cas, on a toujours une probabilité de victoire de 63/101...
Certes, Pixelax donne l'impression de brasser un intervalle moins large en se restreignant à l'intervalle [0 ; 63] alors que Quentin qui brasse carrément tout l'intervalle [0 ; 100] ; mais, dans le premier cas, Pixelax est sûr de trouver si le nombre mystère est bien dans l'intervalle [0 ; 63] alors que dans le second on a prouvé que Quentin devait forcément compter sur la chance à un moment ou à un autre. Le truc, c'est surtout que Pixelax compte sur la chance dès le départ en supposant que le nombre mystère est dans un intervalle restreint là où Quentin va aviser au fur et à mesure, mais sans pour autant avoir la garantie de viser juste (comme le montre l'arbre de Pixelax). Et il a beau avoir eu pas mal de chance quand je l'ai mis au défi de trouver les nombres que j'ai tirés au sort avec Excel, il les a quand même pas tous trouvés, donc bon...

Et ne nous parlez pas de "Mais on sait qu'il va prendre un nombre plus près de 0 ou de 100 car il sera plus difficile à cerner dès le départ", car là, ce ne sont plus des mathématiques, mais du mentalisme. Et se douter que le MJ a un esprit tordu, c'est pas plus stratégique que compter sur la chance à mon sens.

garsim a écrit:Certes, Pixelax donne l'impression de brasser un intervalle moins large en se restreignant à l'intervalle ⟦0, 63⟧ [...]

Presque, on a vu que l'on ne pouvait distinguer que 63 cas, donc je me restreins à ⟦0, 62⟧. En fait c'est même ⟦0, 61⟧ avec les règles de l'épreuve, car si jamais la réponse est 62, je n'aurai eu que des réponses "+", et je saurai juste que le nombre mystère est dans ⟦62, 100⟧. Donc une chance sur 39 seulement de trouver la bonne réponse, le plus sage est de ne pas prendre le risque de finir en prison !



À part ça, deux petites énigmes (indépendantes) posées lors du dernier FBV :


Passe-Muraille et Passe-Partout ont chacun reçu une bourse de boyards. Il se trouve que Passe-Muraille a deux fois plus de boyards que Passe-Partout. Si Passe-Partout donnait 7 boyards à Passe-Muraille, ce dernier en aurait alors 3 fois plus que lui !
Combien Passe-Partout a-t-il reçu de boyards ?


Si je vous dis que dans 11 ans, je serai 15% plus âgé que je ne l'étais il y a 7 ans... quel âge ai-je aujourd'hui ?

Heu, pour la 2e énigme, soit il y a une erreur dans l'intitulé/dans mon raisonnement, soit tu es immortel parce que j'obtiens comme âge actuel 127 ans

rhyolite a écrit:Heu, pour la 2e énigme, soit il y a une erreur dans l'intitulé/dans mon raisonnement, soit tu es immortel parce que j'obtiens comme âge actuel 127 ans

Non non, pas d'erreur ni dans l'énoncé, ni dans le raisonnement : bonne réponse !
Je rappelle que c'était une énigme du Père Fouras, donc 127 ans ce n'est pas choquant ^^

Petites questions - certes posées un peu tard vu le contexte - mais...

1) le nombre 2017 a une particularité que les nombres voisins n'ont pas... le précédent était 2011, le prochain sera 2027. De quoi parle-t-on?


2) cette particularité, je l'ai indiquée lors de mes vœux, notamment à mes amis matheux. Et j'ai eu la réponse suivante d'une algébriste:

Comme [2017 a la particularité ci-dessus, et qu'il] est congru a 1 modulo 4,
il est somme de deux carres. Lequels?

Eh bien je vous pose la question!

Après quelques recherches, je peux en conclure qu'il s'agit de nombres premiers !

Et pour la 2) c'est 9 et 44 :p

L'année 2016 était quand même particulièrement extraordinaire me semble parce que ce nombre est à la fois triangulaire et hexagonal et la dernière année comme ça remonte au 18 ou 19ème siècle.

Ça fait plaisir de voir des non-matheux investir ce topic!

Anonyme a écrit:Après quelques recherches, je peux en conclure qu'il s'agit de nombres premiers !

Chris K. a écrit:Et pour la 2) c'est 9 et 44 :p

Et ce sont deux bonnes réponses!

Bastien a écrit:L'année 2016 était quand même particulièrement extraordinaire me semble parce que ce nombre est à la fois triangulaire et hexagonal et la dernière année comme ça remonte au 18 ou 19ème siècle.

J'ai souhaité mes bons vœux pour l'année (2.2.3.4.6.7) l'an passé

Et effectivement, 2016 est hexagonal: https://oeis.org/A000384 en répertorie la liste... et justifie ton affirmation

bibi6 a écrit:

Comme [2017 a la particularité ci-dessus, et qu'il] est congru a 1 modulo 4,
il est somme de deux carres. Lequels?

Eh bien je vous pose la question!

À ma connaissance, il n'y a pas de méthode plus efficace pour trouver la réponse que tester une à une toutes les possibilités. (Petite question en passant, si on sait que n est premier et congru à 1 modulo 4, combien doit-on faire d'essais au plus pour trouver un a et un b tel que n = a² + b² ?)


La question intéressante est surtout de savoir pourquoi tout nombre premier congru à 1 modulo 4 est somme de deux carrés... mais ce résultat est bien plus difficile que tout ce dont on a pu parler sur ce forum, donc je vais pas rentrer dans les détails.
Plus d'infos sur la page Wikipedia : Théorème des deux carrés de Fermat



Quelque chose de bien plus simple, une question posée il y a quelques temps dans 8 Chances de tout gagner (c'est rare d'avoir une question si orientée maths dans un jeu TV d'ailleurs ^^) :

Et tant que vous y êtes, vous avez même le droit de les ranger par ordre croissant

Du plus petit au plus grand :

11 puissance zéro
4/3
Racine carrée de 2
157x1,01
Valeur absolue de -2
Pi
Racine cubique de 125
Une demi-douzaine

Aïe @Julien, petit souci de recopie pour toi... mais je te rassure, l'ordre est correct!

Pour le nombre maximum de tests de @Pixelax, à la (grosse) louche: l'entier inférieur ou égal à $\sqrt{n/2}$. Mais je suis persuadé qu'il y a moyen de faire mieux, en s'y prenant bien ^^

Pixelax a écrit:La question intéressante est surtout de savoir pourquoi tout nombre premier congru à 1 modulo 4 est somme de deux carrés... mais ce résultat est bien plus difficile que tout ce dont on a pu parler sur ce forum, donc je vais pas rentrer dans les détails.

Juste un peu

AH oui en effet xD Bon ça change rien après ^^

Pour la question de 8 Chances, effectivement c'était pas très compliqué ^^

bibi6 a écrit:Pour le nombre maximum de tests de @Pixelax, à la (grosse) louche: l'entier inférieur ou égal à $\sqrt{n/2}$. Mais je suis persuadé qu'il y a moyen de faire mieux, en s'y prenant bien ^^

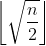C'est bien cette réponse que j'attendais en tout cas : (oui c'est plus joli une fois compilé )

D'après ce qu'on a dit, n s'écrit a² + b², avec a et b entiers naturels. Quitte à changer les notations, supposons a < b (remarquez que comme n est impair, on ne peut pas avoir a = b).
L'idée est de tester pour chaque x si n - x² est un carré ou non. S'il l'est, on a alors a = x et b = √(n - x²), et c'est terminé.
Comme n est premier, a ≠ 0, donc on peut commencer à x = 1. Il suffit de s'arrêter dès que n - x² ⩽ x², puisqu'on a imposé b > a. Cela revient à x ⩾ √(n/2) (remarquons que √(n/2) n'est pas un entier comme n est impair).
On teste donc tous les entiers compris entre 1 et √(n/2) : il y en a exactement .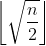


Il y a peut-être moyen de faire mieux, mais je ne vois pas trop comment. Par exemple, pour n = 37, a = 1 ; et pour n = 41,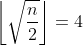 , et on a justement a = 4 (ceci n'est pas du tout une preuve que c'est optimal, juste des exemples qui montrent que a peut être aussi bien minimal que maximal).

Vous vous souvenez qu'un professeur de mathématique avait proposer des questions de géométrie sur le dab de P. Pogba

et bin, il a récidivé et c'est avec le biathlon et Martin Fourcade
Voici les problèmes

@Carlobservateur : Sans vouloir être méchant, le but de ce sujet n'est pas de faire des maths juste pour dire d'en faire ! C'est nettement plus intéressant lorsque les maths sont un outil pour répondre à un problème naturel (cc @garsim). C'est d'ailleurs ce que j'ai presque toujours fait dans ce sujet et dans le jeu Mathématiques boyardesques (à part les énigmes de mon FBV, qui elles étaient totalement artificielles et n'avaient été créées dans le seul but d'être résolubles rapidement - en théorie ^^).

Dans ce que tu postes, le biathlon n'est qu'un prétexte pour faire faire des maths à des collégiens. Si encore le thème avait été Fort Boyard j'aurais compris, mais là ce sont avant tout de simples exos de maths autour desquels on a un peu brodé pour rendre ça un tout petit peu plus ludique (et encore).
Si vous voulez, je peux vous faire partager le dernier devoir que j'ai fait, mais je doute que les formes symplectiques intéressent grand monde ici !



Voilà un exemple de cadre qui est une vraie mine de problèmes mathématiques concrets (et surtout non triviaux) : The Wall !

Pour une fois je ne vais rien ajouter de plus pour le moment. Je trouve que ça peut être intéressant de vous laisser vous poser des questions sur ce nouveau jeu, puis éventuellement essayer d'y répondre en modélisant la situation.
D'ailleurs, même si vous n'avez absolument aucune idée de comment y répondre - et même si vous n'y connaissez rien en maths ^^, n'hésitez pas à poser vos questions qui vous viennent naturellement en tête ici (en rapport avec les maths bien sûr), on essaiera de trouver la solution.

Spoiler: