Coin MATHÉMATIQUES
+11
Carlobservateur
Bastien
Julien
Paul
Peyo13
Anonyme
bibi6
rhyolite
RiverOfBoyards
garsim
Pix
15 participants
Page 8 sur 8
Page 8 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Oui, je devais revenir, et je suis pas revenu... 
Mais j'ai, je pense, l'argument "qui va bien". Mais je laisse les autres réfléchir
[HS]Et concernant les concours, l'agrég "externe spécial" est bien pour les docteurs, et j'ai été voir le CAPES ces deux derniers jours. Et j'ai bien gratté du papier
En résumé, hier: Option info, sudoku et géométrie algorithmique; option math, réseaux et pavages du plan, et involutions sur les réels positifs. Aujourd'hui, pour tous: méthode de Monte-Carlo pour le quart de cercle et PageRank.[/HS]
Mais j'ai, je pense, l'argument "qui va bien". Mais je laisse les autres réfléchir
[HS]Et concernant les concours, l'agrég "externe spécial" est bien pour les docteurs, et j'ai été voir le CAPES ces deux derniers jours. Et j'ai bien gratté du papier
En résumé, hier: Option info, sudoku et géométrie algorithmique; option math, réseaux et pavages du plan, et involutions sur les réels positifs. Aujourd'hui, pour tous: méthode de Monte-Carlo pour le quart de cercle et PageRank.[/HS]
bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Allez, fin du suspense : la méthode de laquelle je parlais utilise le binôme de Newton de manière un peu astucieuse. En fait, il suffit d'écrirePixelax a écrit:De manière générale, on veut donc montrer que
Pour n impair c'est très facile, ça provient directement de la symétrie des coefficients binomiaux. Manque de pot, ici 14 c'est pair !
Pourtant, le résultat tombe en une ligne si on utilise une formule bien pratique qui fait intervenir des coefficients binomiaux...
On sépare les termes pairs et impairs, et le tour est joué !
Je laisse de côté la fin de l'étude de The Wall (notamment les cas où la boule n'est pas lâchée en 4), mais si ça intéresse certains on peut en reparler si vous le souhaitez. ^^
En attendant, un autre problème de probas comme vous aimez ça :
Comme vous l'avez peut-être remarqué, @garsim utilise depuis peu des avatars et signatures aléatoires, qui changent à chaque fois que l'on (re)charge une page. On suppose que les tirages sont effectués de manière indépendante et uniforme sur un ensemble de N éléments différents (on prendra N = 9 pour les avatars et N = 164 pour les signatures).
En moyenne, combien de pages doit-on charger pour avoir vu au moins une fois chaque avatar ? ... chaque signature ? ... chaque couple (avatar + signature) ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Et si je te disais que ce n'était pas le cas et que j'avais programmé mon schmilblic de manière à ce que la signature dépende de l'avatar ?Pixelax a écrit:On suppose que les tirages sont effectués de manière indépendante et uniforme sur un ensemble de N éléments différents (on prendra N = 9 pour les avatars et N = 164 pour les signatures).

(... bon d'accord c'est pas le cas)
Bon, honnêtement, pour le problème (et j'espère que t'as pensé à cliquer sur la signature pour pouvoir la recharger à loisir, parce que c'est plus commode et que ça m'étonnerait que t'aies sorti le 164 du chapeau vu que je n'ai pas dit combien j'en avais
En fait, si je prends un exemple tout bête de "Pile ou face" où l'énoncé serait "En moyenne, combien de fois faut-il lancer la pièce pour qu'on voie au moins une fois pile et au moins une fois face ?", ce que je vais trouver étrange, c'est qu'il peut exister un cas où on ne tombera jamais sur face même en lançant la pièce un grand nombre de fois (même s'il deviendra de moins en moins probable au fur et à mesure des lancers).
Faudrait-il alors considérer un epsilon > 0 tel que P(jamais tombé sur face) < epsilon à partir duquel on peut estimer que c'est bon, la proba devient nulle ?
Pour l'instant, tout ce que j'ai, pour les avatars, c'est que la proba d'avoir les 9 différents en 9 tentatives est de 9! / 99 (pour les signatures, ce sera 164! / 164164 ; et pour le combo des deux, 1476! / 14761476).
Je ne sais pas si ça peut être utile à la résolution de ton problème...
(et je précise à toutes fins utiles que mes signatures ne sont pas des Pokémon, le but n'est pas de toutes les visualiser !

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Le problème que tu considères est le même que celui proposé, pour N = 2. C'est une bonne idée de déjà comprendre celui-là avant de chercher pour N quelconque ^^garsim a écrit:En fait, si je prends un exemple tout bête de "Pile ou face" où l'énoncé serait "En moyenne, combien de fois faut-il lancer la pièce pour qu'on voie au moins une fois pile et au moins une fois face ?", ce que je vais trouver étrange, c'est qu'il peut exister un cas où on ne tombera jamais sur face même en lançant la pièce un grand nombre de fois (même s'il deviendra de moins en moins probable au fur et à mesure des lancers).
En effet, il y a une petite différence avec les autres problèmes de probas que j'ai posés jusqu'à présent : si on note TN la variable aléatoire correspondant au premier temps où l'on l'on a vu tous les éléments au moins uns fois (on a donc TN ⩾ N), elle n'est pas bornée, et peut même a priori prendre comme valeur +∞.
Pour des cas simples (comme N = 2) on peut faire le calcul explicitement, trouver P(TN=k) et sommer pour k∈ℕ. Si on obtient 1, on peut dire qu'"il n'y a plus de place pour la valeur +∞".
C'est exactement le cas de la loi géométrique, qui est d'ailleurs très proche du cas N = 2.
Elle modélise le problème suivant : on répète une expérience qui a une probabilité p (avec p > 0) de réussir de manière indépendante et on s'intéresse au temps du premier succès, que l'on note X.
On peut déterminer facilement la loi de proba : si X = k, c'est qu'on a eu k-1 échecs (proba 1-p) puis 1 succès (proba p). Comme tous les tirages sont indépendants, on déduit immédiatement que P(X=k) = p(1-p)k-1.
On se rend compte que la suite (P(X=k)) est géométrique (comme par hasard !) de raison 1-p ∈ [0,1[, et est donc sommable. On trouve que cette somme vaut 1 quelque soit p, ce qui prouve que X ne peut pas prendre +∞ comme valeur.
[aparté]De manière générale ce n'est pas parce qu'une variable aléatoire X ne prend que des valeurs finies qu'il en est de même pour son espérance !
Par exemple, si l'on modifie un peu ton problème de pile ou face, et que l'on s'arrête non-pas quand on a eu un pile et un face, mais lorsque le nombre de piles et de faces obtenus deviennent égaux pour la première fois (hors 0 = 0), on peut montrer qu'on a une variable aléatoire qui ne prend que des valeurs finies mais d'espérance infinie.
Ce qui joue en fait, c'est la vitesse de convergence vers 0 de la probabilité que l'on n'ait toujours pas gagné au cours du temps. Sans rentrer dans des considérations plus techniques, on aura une espérance finie si est seulement si cette vitesse de convergence est suffisamment "importante".
À part ça, si la pièce n'est pas équilibrée (la proba de faire pile est différente de 1/2) dans ce même problème, alors la variable aléatoire pourra prendre la valeur +∞ avec une proba non-nulle. Du coup, aucune chance que son espérance soit finie ^^[/aparté]
Ici tout se passe bien, on peut calculer l'espérance d'une variable géométrique facilement. Je vous passe les calculs, mais on montre que E[X] = 1/p.
C'est assez intuitif en fait, en moyenne il faut lancer 1(1/2) = 2 fois une pièce pour obtenir pile et 1/(1/6) = 6 fois un dé pour obtenir "4" par exemple.
Ce résultat joue un rôle clé dans le problème initial. Le but est essayer de se raccrocher le plus possible à cette loi géométrique. Une fois que le lien sera établi, ça montrera que notre variable TN ne peut pas prendre +∞ comme valeur, et ça nous permettra de calculer son espérance... qui sera elle aussi finie.
Du coup non, pas la peine de faire si compliqué ^^garsim a écrit:Faudrait-il alors considérer un epsilon > 0 tel que P(jamais tombé sur face) < epsilon à partir duquel on peut estimer que c'est bon, la proba devient nulle ?
Oui c'est bien ça, mais non ça ne nous aide pas icigarsim a écrit:Pour l'instant, tout ce que j'ai, pour les avatars, c'est que la proba d'avoir les 9 différents en 9 tentatives est de 9! / 99 (pour les signatures, ce sera 164! / 164164 ; et pour le combo des deux, 1476! / 14761476).
Je ne sais pas si ça peut être utile à la résolution de ton problème...
Dans le cas général, l'expression de la loi de proba est un peu lourde, et pas du tout pratique pour calculer son espérance de manière explicite.
La meilleure stratégie est d'essayer de décomposer le problème pour se ramener à ce qu'on connaît (la loi géométrique !), le calcul de l'espérance pourra se faire facilement ensuite. Une fois que vous avez compris les cas N = 2 et N = 3, le cas général ne devrait plus poser de problème.

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je ne reviens pas sur les problèmes précédemment évoqués, mais si ça intéresse du monde je peux donner des indications voire des éléments de réponse bien sûr. 
Un autre problème de probas pour changer :
On dispose d'un dé équilibré à 10 faces, numérotées de 1 à 10 (je rappelle à toutes fins utiles qu'Abraham Lincoln n'est PAS un chiffre entre 1 et 10). On le lance plusieurs fois de suite en additionnant successivement les points obtenus, en ayant commencé à 0 œuf corse. On s'arrête dès que l'on a atteint ou dépassé 21.
Quelle est la probabilité de s'être arrêté exactement sur 21 ?
Un autre problème de probas pour changer :
On dispose d'un dé équilibré à 10 faces, numérotées de 1 à 10 (je rappelle à toutes fins utiles qu'Abraham Lincoln n'est PAS un chiffre entre 1 et 10). On le lance plusieurs fois de suite en additionnant successivement les points obtenus, en ayant commencé à 0 œuf corse. On s'arrête dès que l'on a atteint ou dépassé 21.
Quelle est la probabilité de s'être arrêté exactement sur 21 ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
#Cocalane

Quelle est, en fonction du nombre de boyards, la probabilité que le joueur qui a commencé gagne le duel ?
Hey, en fait tu t'es trompé de sujet @Jonathanlegrand, c'est pas un duel du Conseil, c'est un problème de maths !Jonathanlegrand a écrit:Le faux boyard.
Sur la table se trouve une quinzaines de boyards aligné.le candidat et le maître devront chacun leurs tours choisir un boyard et le retourné.celui qui tombe sur le boyard qui a une face noire (j'ai choisi le noir pour que sa corresponde au lieu) perd le duel. [ici]
Quelle est, en fonction du nombre de boyards, la probabilité que le joueur qui a commencé gagne le duel ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Alors, de ce que j'ai pu trouver, la probabilité serait celle-ci pour un duel à n boyards :
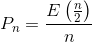
Mais je vais attendre que tu le confirmes pour essayer de me lancer dans une démonstration au cas où ce serait une mauvaise réponse bon, en fait c'est aussi parce que je vois pas encore comment faire une démonstration en bonne et due forme
Toujours est-il que, du coup, si ce résultat est confirmé, on aurait toujours une probabilité de 0,5 pour un nombre de boyards pair, et une probabilité défavorable pour celui qui commence pour un nombre de boyards impair...
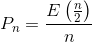
Mais je vais attendre que tu le confirmes pour essayer de me lancer dans une démonstration au cas où ce serait une mauvaise réponse bon, en fait c'est aussi parce que je vois pas encore comment faire une démonstration en bonne et due forme
Toujours est-il que, du coup, si ce résultat est confirmé, on aurait toujours une probabilité de 0,5 pour un nombre de boyards pair, et une probabilité défavorable pour celui qui commence pour un nombre de boyards impair...

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je confirme la réponse. Maintenant plus d'excuse, j'attends la démogarsim a écrit:Alors, de ce que j'ai pu trouver, la probabilité serait celle-ci pour un duel à n boyards :
Mais je vais attendre que tu le confirmes pour essayer de me lancer dans une démonstration au cas où ce serait une mauvaise réponse bon, en fait c'est aussi parce que je vois pas encore comment faire une démonstration en bonne et due forme
Mais comment tu as trouvé le résultat d'ailleurs, si tu n'as pas vraiment de preuve en tête ?
En effet. Et dans le cas impair, plus il y a de boyards plus on se rapproche d'une proba de 0,5 (environ 0,47 pour n = 15).garsim a écrit:Toujours est-il que, du coup, si ce résultat est confirmé, on aurait toujours une probabilité de 0,5 pour un nombre de boyards pair, et une probabilité défavorable pour celui qui commence pour un nombre de boyards impair...

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
J'ai copié la réponse de mon voisin de table sans chercher à la comprendre, pourquoi ?Pixelax a écrit:Mais comment tu as trouvé le résultat d'ailleurs, si tu n'as pas vraiment de preuve en tête ?

Bon, en fait, j'avais fait quelques cas de test, puis j'ai extrapolé en voyant la tronche qu'ils avaient.
Je vais tenter de faire une démonstration généralisée :
Déjà, il est plus simple de faire deux cas distincts :
- nombre de pièces pair
- nombre de pièces impair
Avec un nombre de pièces pair, une partie se déroulera comme ça :
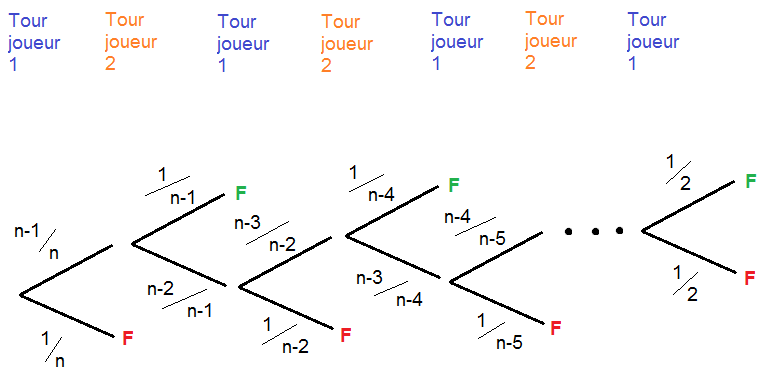
Bon, naturellement, lors du dernier tour, le joueur 2 n'a plus le choix de la pièce.
(le "F" signifie "Fin du jeu" ; en rouge, les cas défavorables pour le joueur 1 ; en vert, ceux favorables pour le joueur 1)
Pour un nombre de pièces impair, c'est pareil, si ce n'est que c'est le joueur 2 qui a le dernier mot dans le cas le plus extrême.
Pour justifier les probabilités présentes, on est d'accord que, si un joueur a le choix entre n pièces dont 1 blanche, il a 1 chance sur n de prendre la blanche et donc n-1/n chances de prendre une vraie pièce.
A son tour, le joueur suivant aura le choix entre n-1 pièces, dont toujours une blanche, avec une probabilité de 1/(n-1) de prendre la blanche et donc (n-1)-1/(n-1) = (n-2)/(n-1) de prendre une vraie.
Puis le joueur suivant aura le choix entre n-2 pièces, etc. Jusqu'à ce qu'il n'en reste plus que deux, avec une probabilité de 1/2 pour chacune.
Pour calculer la probabilité de victoire du joueur 1, il faut sommer le nombre de cas favorables pour lui.
Par exemple, le premier cas favorable (1er "F" vert croisé sur l'arbre) qui va se présenter sera celui où le second joueur prendra la pièce blanche lors de son premier tour, ce qui donne mathématiquement :
Puis le deuxième cas favorable sera donné par cette formule :
Jusqu'à ce qu'on arrive au bout. On obtient donc une formule de ce style :
Et ce qui est génial, c'est qu'on peut simplifier ces fractions toutes de la même manière :
C'est à partir de là que, selon la parité du nombre de pièces initial, le nombre de fois où l'on somme 1/n varie.
Cas pair :
Dans le cas le plus extrême, c'est le joueur 1 qui a le dernier mot. Il pourra donc jouer au maximum n/2 fois :
Or, comme la somme ne dépend pas de notre indice de boucle, on peut factoriser la formule en :
On se retrouve donc dans tous les cas avec une probabilité équivalente entre duellistes pour peu qu'on ait un nombre de pièces pair !
Cas impair :
Ici, c'est le joueur 2 qui a potentiellement le dernier mot. Donc le joueur 1 ne pourra jouer au maximum qu'en-dessous de n/2 fois.
Du coup, pas le choix, on va devoir passer par une fonction partie entière pour le matérialiser (le nombre de tours total maximal ne tombant pas juste, le joueur 1 aura E(n/2) coups et le joueur 2 E(n/2) + 1) :
Là encore, on peut factoriser :
... mais à cause de cette fichue partie entière, on ne peut pas aller plus loin, et la probabilité dépendra donc du nombre de pièces initial pour le cas impair.
La formule du cas impair fonctionne aussi très bien pour le cas pair ; c'est juste que dans ce cas-là, E(n/2) = n/2 vu que n est pair, et qu'on peut donc simplifier directement. On élimine d'ailleurs le fait que la probabilité soit calculée en fonction de n.

"Fort Boyard, on oublie toute notre dignité" - Lenni-Kim, 2019

garsim- Fan-Imbattable

- Inscription : 20/05/2015
Messages : 3243
Boyards : 3199
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je me demandais justement si t'allais choisir la méthode qui fait deux pages ou celle qui fait deux lignes. Mais je me doutais bien que tu n'allais pas pouvoir résister à l'occasion de poster un joli pavé ! 
Tout ce que tu as fait semble bon, et ça en fait une démonstration (quasi) rigoureuse. Je salue le travail effectué car ça a dû te prendre du temps de formaliser tout ça, et surtout de le présenter de manière jolie.
Néanmoins, comme je le disais plus haut, il y a une méthode bien plus simple. Elle ne nécessite aucun calcul, ni même aucun arbre ou quoi que ce soit dans ce style. Comme souvent en probas, il faut essayer de voir le problème sous le bon angle...
J'en dis pas plus pour le moment, à vous de la trouver. =)
Tout ce que tu as fait semble bon, et ça en fait une démonstration (quasi) rigoureuse. Je salue le travail effectué car ça a dû te prendre du temps de formaliser tout ça, et surtout de le présenter de manière jolie.
Néanmoins, comme je le disais plus haut, il y a une méthode bien plus simple. Elle ne nécessite aucun calcul, ni même aucun arbre ou quoi que ce soit dans ce style. Comme souvent en probas, il faut essayer de voir le problème sous le bon angle...
J'en dis pas plus pour le moment, à vous de la trouver. =)

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Bonsoir à tous,
Ça fait un peu déterrage de topic, et occulter le problème de @Pixelax, mais en même temps, ça fait 5 mois qu'il est dans cet état, et résolu d'une certaine façon par @garsim ^^
Mais, tout de même, ceci a sa place ici:
Voyez-vous en quoi cela crée un paradoxe? En est-ce réellement un?
(Bien évidemment, Pix, ne dis rien! )
)
Ça fait un peu déterrage de topic, et occulter le problème de @Pixelax, mais en même temps, ça fait 5 mois qu'il est dans cet état, et résolu d'une certaine façon par @garsim ^^
Mais, tout de même, ceci a sa place ici:
Dans le sujet \"Poisson d'avril 2018", Pixelax a écrit:C'est un joli paradoxe ça, puisque tu as posté cette phrase dans ce sujet justementJonathan a écrit:Tous ce qui est dit dans ce sujet est un poisson d'avril.
Voyez-vous en quoi cela crée un paradoxe? En est-ce réellement un?
(Bien évidemment, Pix, ne dis rien!

bibi6- Fan-Passionnément

- Inscription : 16/06/2016
Messages : 1024
Boyards : 1275
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Ok ok je ne dis rien alors 
Encore un autre problème, si vous vous ennuyez :
Dans le jeu Qui est la taupe ?, n + 1 candidats doivent coopérer pour remporter un maximum d'argent, mais parmi eux se cache une taupe qui a pour but de faire échouer le groupe. À la fin (en supposant qu'il n'y ait pas eu d'élimination), les candidats doivent démasquer la taupe pour gagner. Chacun fait son choix individuellement, et on supposera que ces choix sont faits au hasard, uniformément parmi les n autres candidats, et de manière indépendante. La taupe gagne si et seulement si personne ne l'a démasquée.
Vous voyez-venir la question : Quelle est la probabilité que la taupe gagne ?
Pour aller plus loin : Comment se comporte cette proba quand on augmente le nombre de personnes ?
Vous pouvez essayer d'intuiter la réponse à la deuxième question avant même de chercher la première : à votre avis, elle augmente, elle diminue, elle oscille, elle se rapproche de 0, de 1, d'une autre valeur, c'est chaotique, ... ?
Encore un autre problème, si vous vous ennuyez :
Dans le jeu Qui est la taupe ?, n + 1 candidats doivent coopérer pour remporter un maximum d'argent, mais parmi eux se cache une taupe qui a pour but de faire échouer le groupe. À la fin (en supposant qu'il n'y ait pas eu d'élimination), les candidats doivent démasquer la taupe pour gagner. Chacun fait son choix individuellement, et on supposera que ces choix sont faits au hasard, uniformément parmi les n autres candidats, et de manière indépendante. La taupe gagne si et seulement si personne ne l'a démasquée.
Vous voyez-venir la question : Quelle est la probabilité que la taupe gagne ?
Pour aller plus loin : Comment se comporte cette proba quand on augmente le nombre de personnes ?
Vous pouvez essayer d'intuiter la réponse à la deuxième question avant même de chercher la première : à votre avis, elle augmente, elle diminue, elle oscille, elle se rapproche de 0, de 1, d'une autre valeur, c'est chaotique, ... ?

×

Pix- Fan-Imbattable

- Inscription : 26/01/2015
Messages : 3644
Boyards : 8107
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Tiens, je suis content de voir ce sujet 
D'ailleurs, les maths j'adore ça, au point que je veux devenir prof de cette matière
Peut-être qu'il y'en a d'autres qui aiment ça... visiblement oui au vu des problèmes que j'ai trouvé
D'ailleurs, les maths j'adore ça, au point que je veux devenir prof de cette matière
Peut-être qu'il y'en a d'autres qui aiment ça... visiblement oui au vu des problèmes que j'ai trouvé

Membre du forum depuis le 7 juin 2021
Modérateur Junior des sections "Épreuves et aventures" et "Jeux de Fort Boyard le Forum" depuis le 3 avril 2024
Moi et Fort Boyard depuis 2009

JujuFortBoyard- Modérateur junior

- Inscription : 07/06/2021
Messages : 2894
Boyards : 1596
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Oui, moi aussi je compte faire des études dans le domaine pour peut-être (mais ce n'est pas sûr du tout) devenir prof.
Bon et puis pour le problème de 2018 ( ), c'est un paradoxe car dire que c'est un poisson d'avril puisque comme tout est un poisson d'avril sur le sujet ça n'en est pas un alors que c'est la phrase dite.
), c'est un paradoxe car dire que c'est un poisson d'avril puisque comme tout est un poisson d'avril sur le sujet ça n'en est pas un alors que c'est la phrase dite.
Bon et puis pour le problème de 2018 (

Vive le Fort

Liarou- Fan-Illuminé(e)

- Inscription : 09/08/2022
Messages : 468
Boyards : 302
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
Je suis en train de rêver là...Liarou a écrit:Oui, moi aussi je compte faire des études dans le domaine pour peut-être (mais ce n'est pas sûr du tout) devenir prof.
Bon et puis pour le problème de 2018 (), c'est un paradoxe car dire que c'est un poisson d'avril puisque comme tout est un poisson d'avril sur le sujet ça n'en est pas un alors que c'est la phrase dite.
Tu voudrais faire prof de maths ? Moi aussi si c'est le cas
Je suis pas encore très sûr mais... disons que j'aimerais bien

Membre du forum depuis le 7 juin 2021
Modérateur Junior des sections "Épreuves et aventures" et "Jeux de Fort Boyard le Forum" depuis le 3 avril 2024
Moi et Fort Boyard depuis 2009

JujuFortBoyard- Modérateur junior

- Inscription : 07/06/2021
Messages : 2894
Boyards : 1596
 Re: Coin MATHÉMATIQUES
Re: Coin MATHÉMATIQUES
C'est une possibilité mais c'est très loin d'être sûr, ce qui est sûr c'est ce que je ferai dans les sciences et plus précisément les maths qui est ma passion depuis que je suis petit.

Vive le Fort

Liarou- Fan-Illuminé(e)

- Inscription : 09/08/2022
Messages : 468
Boyards : 302
JujuFortBoyard est d'accord avec ce message
Page 8 sur 8 •  1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8
Page 8 sur 8
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Accueil
Accueil S'enregistrer
S'enregistrer Connexion
Connexion bibi6 Mar 4 Avr 2017 - 22:13
bibi6 Mar 4 Avr 2017 - 22:13