Mathématiques boyardesques

hélium a écrit:Enfin bref, si j'ai bien compris le principe, ça voudrait dire que le nombre de cas où on aurait quatre billes de chaque est donné par la formule :


Donnant ainsi une probabilité de 6,52 % ?

Tu as bien compris, c'est une bonne réponse !
Je vais rapidement détailler chaque méthode :

- Si les billes sont numérotées on a 12! possibilités, mais comme les permutations des billes d'une même couleur ne changent pas la combinaison, on doit diviser par 4! pour chaque couleur, soit (4!)³. On obtient finalement 34650.

- Il y a possibilités pour les billes rouges, restent 8 trous pour les noires et les blanches. Parmi ces 8 trous, choix pour les noires, les blanches sont ensuite imposées. Le résultat est le produit des deux, soit 34650.

-

hélium a écrit:Euuuh... sincèrement, je ne pensais pas que ça existait mais en fait si, en tapant "coefficients trinomiaux" dans Google, on a bien des résultats. J'ai du mal à y croire.  
Mais, va savoir pourquoi, on n'a quasiment que des résultats en anglais, hormis l'article Wikipédia... mais je suis tombé sur une page très intéressante et plus explicite qui semble effectivement donner la méthode instantanée pour calculer ça. Je me demande pourquoi on n'a jamais étudié ça d'ailleurs... que ce soit en terminale ou dans les quelques cours de maths post-bac que j'ai eus, d'autant plus que certains parlaient de probabilités...

"Coefficients trinomiaux" je n'en ai jamais entendu parler non plus, on parle en fait directement de coefficients multinomiaux ^^ Et c'est en effet assez utile en dénombrement / probas discrètes, comme ici.
On trouve en effet 34650, par la même formule que dans la première méthode finalement.

D'où, en divisant par 3¹², une proba d'environ 6,5 % (et pourtant, c'est arrivé dans la grande majorité des fois où ce duel a été joué!).


Petit point sur le classement, hélium creuse à nouveau l'écart !

Classement provisoire :

Troisième et dernière question de ce problème :

On suppose toujours que le Père Fouras choisit la combinaison au hasard, et on se place dans les mêmes conditions qu'en 2011 (comme sur la photo) : les duellistes n'ont à leur disposition que 5 billes rouges, 4 biles blanches, et 5 billes noires.

c) Quelle est la probabilité que la combinaison soit reproductible par les duellistes ? (5 pts)

Là on ne peut dire que la question n'est a priori pas évidente, mais maintenant que vous maîtrisez parfaitement les coefficients multinomiaux, ça ne devrait pas vous poser trop de soucis

Pixelax a écrit:maintenant que vous maîtrisez parfaitement les coefficients multinomiaux, ça ne devrait pas vous poser trop de soucis

Euh, attends, c'est pas parce que je lis une page sur Internet trouvée au hasard que je deviens incollable à ce sujet...


Sinon, c) : 0,26 % ?

hélium a écrit:

Pixelax a écrit:maintenant que vous maîtrisez parfaitement les coefficients multinomiaux, ça ne devrait pas vous poser trop de soucis

Euh, attends, c'est pas parce que je lis une page sur Internet trouvée au hasard que je deviens incollable à ce sujet...

Ah bon ?
Plus sérieusement, il n'y a pas besoin d'énormément de théorie ici, l'expression du coefficient suffit largement ^^

hélium a écrit:Sinon, c) : 0,26 % ?

Non, mauvaise réponse

Une condition suffisante pour que la combinaison soit réalisable est (par exemple) qu'elle soit composée de 4 billes de chaque couleur ; la proba recherchée est donc d'au moins 6,5 %

Pixelax a écrit:Là on ne peut dire que la question n'est a priori pas évidente

(j'en profite pour corriger ma faute de frappe, faute de pouvoir éditer ^^
Si je dis ça, c'est parce que si on essaye de résoudre ce problème dans le cas général, la formule devient vite ingérable (à moins de torturer son ordi ^^). Si il y avait eu ne serait-ce qu'une bille de chaque couleur en plus autorisée (au lieu de 5/4/5), les calculs auraient été beaucoup plus lourds.
Là, on s'en sort assez facilement puisque presque toutes les billes sont utilisées, il suffit de faire la liste des cas possibles, et d'additionner toutes les possibilités pour avoir le nombre d'issues total.

Ok...

Si je n'ai oublié aucun cas, je pense que ça devrait donc donner c) = 30,51% ...

hélium a écrit:Si je n'ai oublié aucun cas, je pense que ça devrait donc donner c) = 30,51% ...

Le compte est bon ! bonne réponse !

Le détail avec tous les cas possibles (la dernière colonne est obtenue en prenant le coefficient multinomial des trois paramètres (dont la somme fait toujours 12 bien sûr) parmi 12.



D'où une proba de 162162/3¹², ce qui nous fait environ 30,5 %. Le Père Fouras a plutôt intérêt à ne pas choisir au hasard s'il ne veut pas avoir des surprises ^^

Au niveau du classement, l'avance d'hélium devient vraiment importante :

Classement provisoire :

Tellement importante que ça va être vraiment difficile de le rattraper, vu qu'il a 11 points d'avance et que nous arrivons au dernier problème qui ne peut rapporter qu'au plus 10 points

Problème 11 - Les dés

Pour changer, voici un problème de probas ^^
Rassurez-vous, rien de bien sophistiqué, pas besoin de factorielles ou de coefficients machinnomiaux (enfin, on peut s'en servir quand même si vous y tenez vraiment), vous pouvez entièrement vous en sortir avec des arbres

Pour simplifier, on va supposer que l'on n'effectue qu'un seul lancer de dés, et que si plusieurs combinaisons sont vérifiées en même temps, seule la plus forte compte. Par exemple, AABCA n'est pas une paire, mais un brelan (on croirait que ça rend les choses plus difficiles, mais c'est tout le contraire, c'est bien plus facile comme ça ^^).

a) Quelle est la probabilité que la combinaison obtenue ne rentre pas dans le tableau ? (1 pt)

b) Quelle est la probabilité d'obtenir chacune des combinaisons du tableau ? (7 × 1 pt)
Vous l'aurez compris, j'attends une liste de 7 valeurs pour cette réponse ; si seulement une partie est correcte, vous aurez une partie des points au prorata de vos bonnes réponses.


Et là, un truc vraiment amusant. Il paraîtrait logique que le tableau soit ordonné de la combinaison la plus probable (pour la plus faible) à la moins probable (la plus forte)... mais le Père Fouras a dû sécher les cours de probas dans sa jeunesse, puisque ce n'est pas le cas !

c) Quel est alors le tableau des combinaisons correctement ordonné ? (2 pts)
Je vous l'accorde, une fois que vous avez la b), la c) est immédiate. Prenez ça comme un bonus si vous trouvez tout !

b) Pour le cinq/cinq : 1/1296 ?

hélium a écrit:b) Pour le cinq/cinq : 1/1296 ?

Oui, bonne réponse !
D'ailleurs, pour tout ce problème, je crois que c'est mieux de ne parler qu'en valeurs exactes

Ça te fait donc un point de plus :

Classement provisoire :

Il reste 6 points à prendre sur la b) !

b) Pour le carré, j'ai un doute mais je tente : 5/2592 ?

hélium a écrit:b) Pour le carré, j'ai un doute mais je tente : 5/2592 ?

Non, mauvaise réponse

Comme je le disais, on peut s'en sortir avec des arbres. On fait donc comme si on lançait les 5 dés les uns après les autres.
Si vous essayez de faire un arbre de manière "naïve", vous allez avoir 6⁵ branches, c'est-à dire 7776. C'est un peu beaucoup ^^

Le mieux est donc d'épurer les arbres au maximum, en étiquetant les faces au fur et à mesure qu'elles sortent. C'est-à-dire qu'on appellera A le premier symbole sorti, B le deuxième, etc. Ainsi, le premier lancé de dé n'apparaîtra pas dans l'arbre, puisqu'il donnera A quoi qu'il arrive ! Le deuxième lancé de dé donnera A dans un cas sur 6, et B dans 5 cas sur 6.
Et pour qu'on y voie encore plus clair, il vaut mieux faire un arbre pour chaque combinaison recherchée, et ne pas écrire les branches qui feront perdre dans tous les cas (par exemple, si on commence par AB, c'est mal barré pour le cinq/cinq ! ).

Par exemple, si on recherche la proba de faire une paire avec 3 dés, voici l'arbre qu'on aurait :

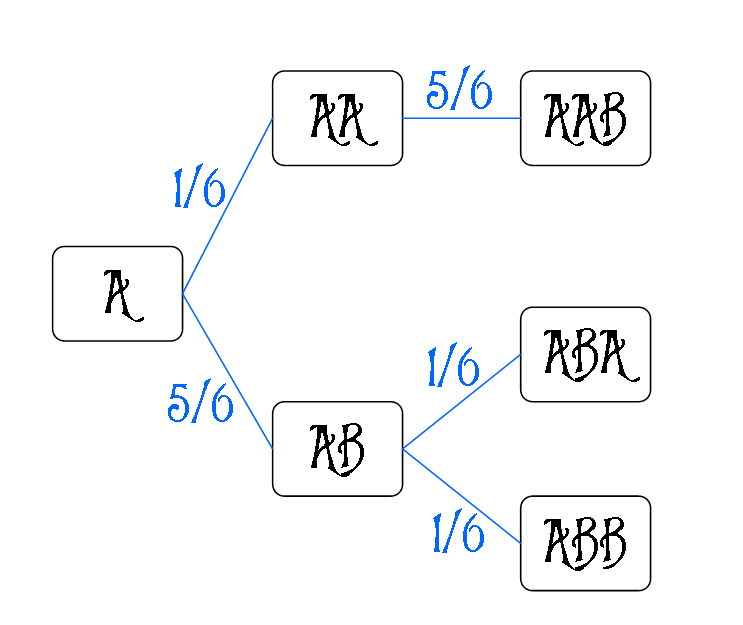
D'où une proba de 1/6 × 5/6 + 5/6 × (1/6 + 1/6) = 15/36. Vous remarquerez qu'on n'a que 3 branches en tout, alors que de manière bourrine on en aurait eu 6³ = 216...!

Avec 5 dés, ça ne change rien au raisonnement, c'est juste un petit peu plus long ^^


Après, je ne vous cacherai pas que la méthode la plus efficace est encore une fois le dénombrement, mais comme vous ne semblez pas très à l'aise avec, je préfère insister sur les arbres, qui sont plus "sûrs"

Pixelax a écrit:la méthode la plus efficace est encore une fois le dénombrement, mais comme vous ne semblez pas très à l'aise avec

Tu comprends maintenant pourquoi je demandais si on allait encore avoir du dénombrement pour le dernier problème ?

Donc je reprends : b) Pour le carré : 13/648 ?

hélium a écrit:Donc je reprends : b) Pour le carré : 13/648 ?

Presque... mais pas, mauvaise réponse

Pixelax a écrit:Pour simplifier, on va supposer que l'on n'effectue qu'un seul lancer de dés, et que si plusieurs combinaisons sont vérifiées en même temps, seule la plus forte compte. Par exemple, AABCA n'est pas une paire, mais un brelan (on croirait que ça rend les choses plus difficiles, mais c'est tout le contraire, c'est bien plus facile comme ça ^^)

En fait, quand je disais que ça simplifiait les calculs, c'est surtout pour la méthode de dénombrement. Pour les arbres, ça ne change pas grand chose, il suffit de bien faire attention (comme dans le cas d'une paire avec 3 dés, lorsqu'on avait AA, je n'ai prolongé la branche que par AAB, et pas par AAA).

Et un conseil : ici, ne simplifiez pas vos fractions, gardez le dénominateur égal à 6⁴ = 1296, sinon ça va pas être pratique pour les comparer (ce qui est quand même le but à terme).

Sinon, elle ne vous plaît pas ma question a) ? Elle ne vaut qu'un point vous savez, ne vous attendez pas à quelque chose d'insurmontable ^^

hélium a écrit:

Pixelax a écrit:la méthode la plus efficace est encore une fois le dénombrement, mais comme vous ne semblez pas très à l'aise avec

Tu comprends maintenant pourquoi je demandais si on allait encore avoir du dénombrement pour le dernier problème ?  

Ceci dit, rien ne vous interdit d'utiliser du dénombrement, c'est plus facile que dans le problème précédent d'ailleurs

Pixelax a écrit:Sinon, elle ne vous plaît pas ma question a) ? Elle ne vaut qu'un point vous savez, ne vous attendez pas à quelque chose d'insurmontable ^^

En même temps, toutes celles de la b) valent aussi un point, donc bon...

Mais maintenant que tu le dis... pour la a), c'est pas tout simplement zéro ? Vu qu'on a six valeurs possibles pour les dés, on a forcément soit une suite, soit au moins une paire...

hélium a écrit:Mais maintenant que tu le dis... pour la a), c'est pas tout simplement zéro ? Vu qu'on a six valeurs possibles pour les dés, on a forcément soit une suite, soit au moins une paire...

Bah si justement, bonne réponse !

Classement provisoire :

hélium a écrit: Mais maintenant que tu le dis... pour la a), c'est pas tout simplement zéro ? Vu qu'on a six valeurs possibles pour les dés, on a forcément soit une suite, soit au moins une paire...

Heu, je suis peut-être complètement à côté de la plaque, mais si on obtient quelque chose du genre 12346 ou 12456, ça ne rentre pas dans le tableau non? On a 6 valeurs pour 5 dés et pas l'inverse

Corrigez-moi si je me trompe, j'ai jamais aimé les probabilités

rhyolite a écrit:Heu, je suis peut-être complètement à côté de la plaque, mais si on obtient quelque chose du genre 12346 ou 12456, ça ne rentre pas dans le tableau non? On a 6 valeurs pour 5 dés et pas l'inverse

Corrigez-moi si je me trompe, j'ai jamais aimé les probabilités

Certes, mais là, ce n'est pas vraiment un poker, même si les règles s'en rapprochent.
Dans le duel des dés, les valeurs ne sont pas ordonnées, donc la "suite" désigne tout simplement une combinaison de cinq dés différents.
Et effectivement, le terme "suite", sans doute choisi pour évoquer l'inspiration du poker, n'est pas vraiment approprié du coup... mais ça, c'est au Père Fouras qu'il faut le dire.

Je ne sais pas trop comment vous aider davantage... Le mieux est vraiment de reprendre la même méthode que je vous ai montrée pour la proba d'une paire avec 3 dés : en faisant des arbres "intelligents", c'est-à-dire en regroupant les cas similaires et en éliminant les cas défavorables, de manière à diminuer considérablement le nombre de branches. C'est que de la logique ^^
Sur les 6 probas qu'il reste à trouver, le plus petit arbre n'a qu'une seule branche (si si !), et le plus grand en à 15 (ce qui reste gérable, surtout qu'il y a des groupes de branches qui se ressemblent fortement).

Je complèterai ce tableau au fur et à mesure :


Comme je l'ai dit, j'attends seulement les valeurs exactes, pas nécessairement simplifiées (de la forme truc/6⁴, truc correspond à la deuxième colonne du tableau). Dans la troisième colonne, j'ajouterai la valeur approchée à 0,1% près, histoire d'avoir une idée de ce que ça représente.


Je donnerai les réponses manquantes (s'il y en a ^^) au plus tard jeudi prochain, ce qui mettra fin au jeu.