Mathématiques boyardesques

J'ai fait une erreur de calcul, je propose donc aussi 1/4060

hélium a écrit:a) 1/30, tout bêtement ?

Chris K. a écrit:J'ai fait une erreur de calcul, je propose donc aussi 1/4060

Mauvaises réponses
La réponse ne demande pas de calcul, il faut juste analyser ce qu'il se passe ^^

Je tente 1/27

rhyolite a écrit:Je tente 1/27

Vous vous rapprochez tout doucement... Mais c'est une mauvaise réponse à nouveau...
Vous allez bien finir par y arriver ^^

1/28 ? 

hélium a écrit:1/28 ?

Ah, là vous refroidissez ! Mauvaise réponse...
Je comprends pas, vous avez répondu à des question bien plus difficiles, et vous bloquez sur un truc tout bête ^^

0 il a pas le temps xd

Chris K. a écrit:0 il a pas le temps xd

Mais non, y a pas de piège !
C'est encore une mauvaise réponse... La réponse n'est pas 1 non plus, rassurez-vous.

Si ça peut vous aider, toutes les réponses que vous avez proposées sont en dessous de celle que j'attends. Et je rappelle qu'il n'y a aucun calcul à faire...

Je tente 1/10, même si ça me parait bizarre qu'on ait à faire aucun calcul...

maximax a écrit:Je tente 1/10, même si ça me parait bizarre qu'on ait à faire aucun calcul...

OUI ! C'est une bonne réponse !
Quelques explications s'imposent on dirait ^^

Le mieux est de faire comme pour le jeu de la Sauvageonne : si le candidat va jusqu'au bout, il a 1 chance sur 9 de gagner, puisque ça revient à ce qu'il choisisse le boyard qu'il ne retournera pas.
Ici c'est pareil ! Le candidat choisit dans quel ordre il essaye les clés ; en particulier il choisit la clé qu'il essaiera en dernier... Il aura donc à essayer les 30 clés si et seulement si la clé qu'il essaye en dernier est une des 3 bonnes clés. D'où une proba de 3/30 = 1/10


Au niveau du classement, maximax prend la tête, mais avec une très courte avance :

Classement provisoire:

Vous vous en doutez peut-être vu le peu de points en jeu, ces deux premières questions n'étaient en fait qu'une mise en jambe.
Voici la question vraiment intéressante :

c) En moyenne, combien de clés le candidat devra-t-il essayer ? (5 pts)

Il semblerait que vous ne soyiez pas très inspirés. C'est parce que j'ai mis 5 points que ça vous fait peur ?  

La méthode à adopter ici est la même que pour le jeu des barreaux. Il vaut mieux commencer par trouver la loi du nombre de clés à essayer (appelons ça X pour changer), pour pouvoir ensuite calculer l'espérance.

Trouver la loi revient à déterminer P(X=k) pour k entre 3 et 30. Vous connaissez déjà les extrêmes P(X=3) et P(X=30) avec les deux premières questions, à vous d'essayer de généraliser !
Vu le nombre total de clés, c'est inenvisageable de faire un arbre. Là y a pas le choix : va falloir faire du dénombrement... Déterminez le nombre d'issues totales, et le nombre d'issues favorables pour chaque valeur de k (chaque issue doit être équiprobable, sinon on ne s'en sort pas ^^). Pour cela, le mieux est d'utiliser les coefficients binomiaux (oui, encore eux !).

Pour rappel, le coefficient binomial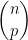 (lire "p parmi n") est le nombre de manières de choisir p éléments parmi n, c'est-à-dire le nombre de manières de faire p croix dans n cases (où chaque case accueille au plus 1 croix).

Y a plus qu'à

Pixelax a écrit:Il semblerait que vous ne soyiez pas très inspirés. C'est parce que j'ai mis 5 points que ça vous fait peur ?  

Essaie de ne mettre qu'un point pour cette question, on verra bien...

En fait, ce qui me bloque, c'est que, par rapport aux barreaux, il faudrait répéter le processus 3 fois... et je vois pas comment modéliser ça.
Pour le nombre d'issues totales, si on utilise les coefficients binomiaux, je pense que ça doit être 4060 (ce qui figurait d'ailleurs dans le résultat trouvé par Chris K.), mais après, pouf ! Quand j'essaie de calculer la proba pour k=4, je tombe sur un truc comme 3/4060, mon petit doigt me dit donc que je m'y prends sans doute mal...

Je tente un petit 10, à pouf comme ça...

hélium a écrit:Je tente un petit 10, à pouf comme ça...

Mauvaise réponse
Pour le coup, c'est vraiment petit oui. ^^ Si on se place dans le cas où il n'y a qu'une bonne clé sur les 30, le candidat a autant de chance de la trouver en n'importe quelle position (entre 1 et 30 donc). Le nombre moyen d'essais est alors de 15,5. Ça ne peut être que plus avec plus de clés à trouver

hélium a écrit:En fait, ce qui me bloque, c'est que, par rapport aux barreaux, il faudrait répéter le processus 3 fois... et je vois pas comment modéliser ça.

Non, pas vraiment. Ou du moins, il ne faut pas voir les choses comme ça, sinon tu ne vas pas t'en sortir ^^
Pour les barreaux, on s'intéressait au moment où le premier palet noir sortait. Là, ce qui importe c'est le moment où la dernière bonne clé est essayée. Le raisonnement est très proche.

hélium a écrit:Pour le nombre d'issues totales, si on utilise les coefficients binomiaux, je pense que ça doit être 4060 (ce qui figurait d'ailleurs dans le résultat trouvé par Chris K.)

C'est une bonne réponse (qui te rapporte 0 point ) ! C'est déjà un bon début. En effet, il n'y a qu'une issue favorable au cas k=3, d'où le 1/4060 qu'on retrouve.

hélium a écrit:Quand j'essaie de calculer la proba pour k=4, je tombe sur un truc comme 3/4060, mon petit doigt me dit donc que je m'y prends sans doute mal...

Parfois, il vaut mieux ne pas écouter son petit doigt.

Pixelax a écrit:C'est une bonne réponse (qui te rapporte 0 point ) !

Ah ben tu vois, là j'étais moins intimidé par ta question à zéro point.

Pixelax a écrit:Parfois, il vaut mieux ne pas écouter son petit doigt.

Oui, il vaut mieux un coup de pouce.

Pixelax a écrit:Là, ce qui importe c'est le moment où la dernière bonne clé est essayée. Le raisonnement est très proche.

Du coup, pour k = 4, on est bien d'accord que ça veut dire que l'épreuve est réussie avec seulement 4 clés essayés, donc une 4^e clé valide, donc trois clés essayées juste avant dont deux valides et une invalide ?
...
...
Oups, attends, en écrivant, je me rends compte que j'avais pas pris en compte le fait qu'on avait une clé en moins à chaque fois.
Je reprends donc : pour k = 4, la probabilité serait bien de (proba que la clé invalide sur 4 soit la 3^e) + (proba que la clé invalide sur 4 soit la 2^e) + (proba que la clé invalide sur 4 soit la 1^re) (on oublie naturellement le cas où la clé invalide sur 4 soit la 4^e vu que ça revient à trouver les 3 clés valides du premier coup)...
Soit : (1/10 * 2/29 * 27/28 * 1/27) + (1/10 * 27/29 * 2/28 * 1/27) + (9/10 * 3/29 * 2/28 * 1/27) ?

D'ailleurs, en suivant ce raisonnement : t'es sûr que pour k = 3, on a bien une proba de 1/10 tout rond ?
De mon côté, j'obtiens 1/10 * 2/29 * 1/28... ou alors il faut vraiment que je change de piste...

hélium a écrit:Du coup, pour k = 4, on est bien d'accord que ça veut dire que l'épreuve est réussie avec seulement 4 clés essayés, donc une 4e clé valide, donc trois clés essayées juste avant dont deux valides et une invalide ?

C'est exactement ça, c'est ce raisonnement qu'il faut utiliser pour déterminer la loi de proba.

L'idée c'est vraiment de compter le nombre d'issues favorables pour un k quelconque (c'est pour ça que je parlais de dénombrement), une fois qu'on a ça c'est gagné puisque toutes les issues sont équiprobables. Il ne faut surtout pas se relancer dans des calculs de probabilités en décomposant clé par clé comme tu l'as fait. En fait, ça revient exactement à faire l'arbre (et des probas conditionnelles, tu te rends compte ? ). Là tu t'en sors parce qu'il y a peu de possibilités, mais ça devient vite ingérable. Tu remarqueras que les trois termes de ta somme sont égaux : c'est normal puisque les issues sont équiprobables !

Je crois que c'est quasiment impossible de trouver le résultat demandé (ou tout au moins de le prouver) sans avoir recours aux coefficients binomiaux. Il ne faut pas avoir peur de les utiliser, au contraire, grâce à eux on trouve la loi de proba sans faire de calculs.
D'ailleurs, c'est tellement puissant qu'on peut simplifier l'expression de l'espérance au point de pouvoir la calculer de tête !

Si ça vous aide, vous pouvez considérer qu'il y a n clés dont p bonnes, le raisonnement est exactement le même. C'est juste qu'ici, contrairement au jeu des barreaux, les valeurs numériques sont plus élevées, donc on ne peut plus analyser tous les cas possibles (ou faire un arbre, c'est pareil).
S'il y avait 1000 clés dont 42 bonnes, le résultat tomberait sans faire de calculs supplémentaires (si ce n'est remplacer n et p par leurs valeurs respectives pour obtenir l'espérance, calculable de tête également).

hélium a écrit:D'ailleurs, en suivant ce raisonnement : t'es sûr que pour k = 3, on a bien une proba de 1/10 tout rond ?

Pour k=30 oui. C'est un moyen de vérifier ta formule d'ailleurs.

En fait, je suis persuadé qu'on peut se ramener à une loi discrète usuelle, mais je vois pas trop laquelle pour le moment. Je pensais à la loi binomiale au départ, mais le problème de la cellule qui rétrécit semble plutôt être similaire à un tirage de Bernoulli sans remise (on ne va pas réessayer les clés qui ont déjà été essayées).
Avec quelques petites recherches, la seule loi qui semble correspondre aux paramètres du problème semble être la loi hypergéométrique (qui, manque de chance, est la seule que je n'ai jamais étudiée à l'école )... mais j'ai un peu de mal à en définir les paramètres dans le cas demandé de calcul de moyenne.

Je pense que je vais revenir quand ce sera un peu plus simple... ^^'